I'm just curious if there's a reason why in order to represent -1 in binary, two's complement is used: flipping the bits and adding 1?
-1 is represented by 11111111 (two's complement) rather than (to me more intuitive) 10000001 which is binary 1 with first bit as negative flag.
Disclaimer: I don't rely on binary arithmetic for my job!
It's done so that addition doesn't need to have any special logic for dealing with negative numbers. Check out the article on Wikipedia.
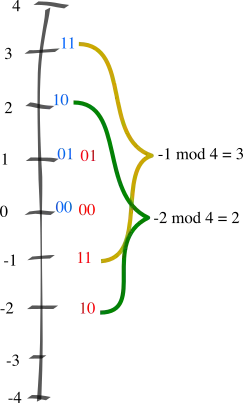
Say you have two numbers, 2 and -1. In your "intuitive" way of representing numbers, they would be 0010 and 1001, respectively (I'm sticking to 4 bits for size). In the two's complement way, they are 0010 and 1111. Now, let's say I want to add them.
Two's complement addition is very simple. You add numbers normally and any carry bit at the end is discarded. So they're added as follows:
0010
+ 1111
=10001
= 0001 (discard the carry)
0001 is 1, which is the expected result of "2+(-1)".
But in your "intuitive" method, adding is more complicated:
0010
+ 1001
= 1011
Which is -3, right? Simple addition doesn't work in this case. You need to note that one of the numbers is negative and use a different algorithm if that's the case.
For this "intuitive" storage method, subtraction is a different operation than addition, requiring additional checks on the numbers before they can be added. Since you want the most basic operations (addition, subtraction, etc) to be as fast as possible, you need to store numbers in a way that lets you use the simplest algorithms possible.
Additionally, in the "intuitive" storage method, there are two zeroes:
0000 "zero"
1000 "negative zero"
Which are intuitively the same number but have two different values when stored. Every application will need to take extra steps to make sure that non-zero values are also not negative zero.
There's another bonus with storing ints this way, and that's when you need to extend the width of the register the value is being stored in. With two's complement, storing a 4-bit number in an 8-bit register is a matter of repeating its most significant bit:
0001 (one, in four bits)
00000001 (one, in eight bits)
1110 (negative two, in four bits)
11111110 (negative two, in eight bits)
It's just a matter of looking at the sign bit of the smaller word and repeating it until it pads the width of the bigger word.
With your method you would need to clear the existing bit, which is an extra operation in addition to padding:
0001 (one, in four bits)
00000001 (one, in eight bits)
1010 (negative two, in four bits)
10000010 (negative two, in eight bits)
You still need to set those extra 4 bits in both cases, but in the "intuitive" case you need to clear the 5th bit as well. It's one tiny extra step in one of the most fundamental and common operations present in every application.
Wikipedia says it all:
The two's-complement system has the advantage of not requiring that the addition and subtraction circuitry examine the signs of the operands to determine whether to add or subtract. This property makes the system both simpler to implement and capable of easily handling higher precision arithmetic. Also, zero has only a single representation, obviating the subtleties associated with negative zero, which exists in ones'-complement systems.
In other words, adding is the same, wether or not the number is negative.
Even though this question is old , let me put in my 2 cents.
Before I explain this ,lets get back to basics. 2' complement is 1's complement + 1 . Now what is 1's complement and what is its significance in addition.
Sum of any n-bit number and its 1's complement gives you the highest possible number that can be represented by those n-bits. Example:
0010 (2 in 4 bit system)
+1101 (1's complement of 2)
___________________________
1111 (the highest number that we can represent by 4 bits)
Now what will happen if we try to add 1 more to the result. It will results in an overflow.
The result will be 1 0000 which is 0 ( as we are working with 4 bit numbers , (the 1 on left is an overflow )
So ,
Any n-bit number + its 1's complement = max n-bit number
Any n-bit number + its 1'complement + 1 = 0 ( as explained above, overflow will occur as we are adding 1 to max n-bit number)
Someone then decided to call 1's complement + 1 as 2'complement. So the above statement becomes: Any n'bit number + its 2's complement = 0 which means 2's complement of a number = - (of that number)
All this yields one more question , why can we use only the (n-1) of the n bits to represent positive number and why does the left most nth bit represent sign (0 on the leftmost bit means +ve number , and 1 means -ve number ) . eg why do we use only the first 31 bits of an int in java to represent positive number if the 32nd bit is 1 , its a -ve number.
1100 (lets assume 12 in 4 bit system)
+0100(2's complement of 12)
___________________________
1 0000 (result is zero , with the carry 1 overflowing)
Thus the system of (n + 2'complement of n) = 0 , still works. The only ambiguity here is 2's complement of 12 is 0100 which ambiguously also represents +8 , other than representing -12 in 2s complement system.
This problem will be solved if positive numbers always have a 0 in their left most bit. In that case their 2's complement will always have a 1 in their left most bit , and we wont have the ambiguity of the same set of bits representing a 2's complement number as well as a +ve number.
Two's complement allows addition and subtraction to be done in the normal way (like you wound for unsigned numbers). It also prevents -0 (a separate way to represent 0 that would not be equal to 0 with the normal bit-by-bit method of comparing numbers).
Two's complement allows negative and positive numbers to be added together without any special logic.
If you tried to add 1 and -1 using your method
10000001 (-1)
+00000001 (1)
you get
10000010 (-2)
Instead, by using two's complement, we can add
11111111 (-1)
+00000001 (1)
you get
00000000 (0)
The same is true for subtraction.
Also, if you try to subtract 4 from 6 (two positive numbers) you can 2's complement 4 and add the two together 6 + (-4) = 6 - 4 = 2
This means that subtraction and addition of both positive and negative numbers can all be done by the same circuit in the cpu.
this is to simplify sums and differences of numbers. a sum of a negative number and a positive one codified in 2's complements is the same as summing them up in the normal way.
The usual implementation of the operation is "flip the bits and add 1", but there's another way of defining it that probably makes the rationale clearer. 2's complement is the form you get if you take the usual unsigned representation where each bit controls the next power of 2, and just make the most significant term negative.
Taking an 8-bit value a7 a6 a5 a4 a3 a2 a1 a0
The usual unsigned binary interpretation is:
27*a7 + 26*a6 + 25*a5 + 24*a4 + 23*a3 + 22*a2 + 21*a1 + 20*a0
11111111 = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
The two's complement interpretation is:
-27*a7 + 26*a6 + 25*a5 + 24*a4 + 23*a3 + 22*a2 + 21*a1 + 20*a0
11111111 = -128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = -1
None of the other bits change meaning at all, and carrying into a7 is "overflow" and not expected to work, so pretty much all of the arithmetic operations work without modification (as others have noted). Sign-magnitude generally inspect the sign bit and use different logic.
To expand on others answers:
In two's complement
Division does require a different mechanism.
All these are true because two's complement is just normal modular arithmetic, where we choose to look at some numbers as negative by subtracting the modulo.
Reading the answers to this question, I came across this comment [edited].
2's complement of 0100(4) will be 1100. Now 1100 is 12 if I say normally. So, when I say normal 1100 then it is 12, but when I say 2's complement 1100 then it is -4? Also, in Java when 1100 (lets assume 4 bits for now) is stored then how it is determined if it is +12 or -4 ?? – hagrawal Jul 2 at 16:53
In my opinion, the question asked in this comment is quite interesting and so I'd like first of all to rephrase it and then to provide an answer and an example.
QUESTION – How can the system establish how one or more adjacent bytes have to be interpreted? In particular, how can the system establish whether a given sequence of bytes is a plain binary number or a 2's complement number?
ANSWER – The system establishes how to interpret a sequence of bytes through types. Types define
EXAMPLE – Below we assume that
char's are 1 byte longshort's are 2 bytes longint's and float's are 4 bytes longPlease note that these sizes are specific to my system. Although pretty common, they can be different from system to system. If you're curious of what they are on your system, use the sizeof operator.
First of all we define an array containing 4 bytes and initialize all of them to the binary number 10111101, corresponding to the hexadecimal number BD.
// BD(hexadecimal) = 10111101 (binary)
unsigned char l_Just4Bytes[ 4 ] = { 0xBD, 0xBD, 0xBD, 0xBD };
Then we read the array content using different types.
unsigned char and signed char// 10111101 as a PLAIN BINARY number equals 189
printf( "l_Just4Bytes as unsigned char -> %hi\n", *( ( unsigned char* )l_Just4Bytes ) );
// 10111101 as a 2'S COMPLEMENT number equals -67
printf( "l_Just4Bytes as signed char -> %i\n", *( ( signed char* )l_Just4Bytes ) );
unsigned short and short// 1011110110111101 as a PLAIN BINARY number equals 48573
printf( "l_Just4Bytes as unsigned short -> %hu\n", *( ( unsigned short* )l_Just4Bytes ) );
// 1011110110111101 as a 2'S COMPLEMENT number equals -16963
printf( "l_Just4Bytes as short -> %hi\n", *( ( short* )l_Just4Bytes ) );
unsigned int, int and float// 10111101101111011011110110111101 as a PLAIN BINARY number equals 3183328701
printf( "l_Just4Bytes as unsigned int -> %u\n", *( ( unsigned int* )l_Just4Bytes ) );
// 10111101101111011011110110111101 as a 2'S COMPLEMENT number equals -1111638595
printf( "l_Just4Bytes as int -> %i\n", *( ( int* )l_Just4Bytes ) );
// 10111101101111011011110110111101 as a IEEE 754 SINGLE-PRECISION number equals -0.092647
printf( "l_Just4Bytes as float -> %f\n", *( ( float* )l_Just4Bytes ) );
The 4 bytes in RAM (l_Just4Bytes[ 0..3 ]) always remain exactly the same. The only thing that changes is how we interpret them.
Again, we tell the system how to interpret them through types.
For instance, above we have used the following types to interpret the contents of the l_Just4Bytes array
unsigned char: 1 byte in plain binarysigned char: 1 byte in 2's complementunsigned short: 2 bytes in plain binary notationshort: 2 bytes in 2's complementunsigned int: 4 bytes in plain binary notationint: 4 bytes in 2's complementfloat: 4 bytes in IEEE 754 single-precision notation[EDIT] This post has been edited after the comment by user4581301. Thank you for taking the time to drop those few helpful lines!
Two's complement is used because it is simpler to implement in circuitry and also does not allow a negative zero.
If there are x bits, two's complement will range from +(2^x/2+1) to -(2^x/2). One's complement will run from +(2^x/2) to -(2^x/2), but will permit a negative zero (0000 is equal to 1000 in a 4 bit 1's complement system).
There are three common methods to represent negative representation of a number which are as below
To understand why 2's Complement is preferred over other two, let us see what limitations other methods posses.
Problem while using Signed bit:
Problem while using 1's Complement:
In 1's Complement, negative number is represented by reversing the bits of its positive representation.
Problem is same as there will two representations of zero i.e minus and plus zero. This will reduce the range as well as create confusion in arithmetic operations.
How 2's Complement solve the issue
Note: Any carry bit at the end is discarded while calculating 2's Complement.
Arithmetic operations are easier to perform, because 2’s complement form is derived from idea of 0-x where x is the number (positive form).
Leading bit is always 1 for the negative number and 0 for the positive number.
It's worthwhile to note that on some early adding machines, before the days of digital computers, subtraction would be performed by having the operator enter values using a different colored set of legends on each key (so each key would enter nine minus the number to be subtracted), and press a special button would would assume a carry into a calculation. Thus, on a six-digit machine, to subtract 1234 from a value, the operator would hit keys that would normally indicate "998,765" and hit a button to add that value plus one to the calculation in progress. Two's complement arithmetic is simply the binary equivalent of that earlier "ten's-complement" arithmetic.
The advantage of performing subtraction by the complement method is reduction in the hardware
complexity.The are no need of the different digital circuit for addition and subtraction.both
addition and subtraction are performed by adder only.
I have a slight addendum that is important in some situations: two's compliment is the only representation that is possible given these constraints:
To see why, it helps to reduce the cardinality; for example, Z_4.
Sign and magnitude and ones' compliment both do not form a ring with the same number of elements; a symptom is the double zero. It is therefore difficult to work with on the edges; to be mathematically consistent, they require checking for overflow or trap representations.
Well, your intent is not really to reverse all bits of your binary number. It is actually to subtract each its digit from 1. It's just a fortunate coincidence that subtracting 1 from 1 results in 0 and subtracting 0 from 1 results in 1. So flipping bits is effectively carrying out this subtraction.
But why are you finding each digit's difference from 1? Well, you're not. Your actual intent is to compute the given binary number's difference from another binary number which has the same number of digits but contains only 1's. For example if your number is 10110001, when you flip all those bits, you're effectively computing (11111111 - 10110001).
This explains the first step in the computation of Two's Complement. Now let's include the second step -- adding 1 -- also in the picture.
Add 1 to the above binary equation:
11111111 - 10110001 + 1
What do you get? This:
100000000 - 10110001
This is the final equation. And by carrying out those two steps you're trying to find this, final difference: the binary number subtracted from another binary number with one extra digit and containing zeros except at the most signification bit position.
But why are we hankerin' after this difference really? Well, from here on, I guess it would be better if you read the Wikipedia article.
A major advantage of two's-complement representation which hasn't yet been mentioned here is that the lower bits of a two's-complement sum, difference, or product are dependent only upon the corresponding bits of the operands. The reason that the 8 bit signed value for -1 is 11111111 is that subtracting any integer whose lowest 8 bits are 00000001 from any other integer whose lowest 8 bits are 0000000 will yield an integer whose lowest 8 bits are 11111111. Mathematically, the value -1 would be an infinite string of 1's, but all values within the range of a particular integer type will either be all 1's or all 0's past a certain point, so it's convenient for computers to "sign-extend" the most significant bit of a number as though it represented an infinite number of 1's or 0's.
Two's-complement is just about the only signed-number representation that works well when dealing with types larger than a binary machine's natural word size, since when performing addition or subtraction, code can fetch the lowest chunk of each operand, compute the lowest chunk of the result, and store that, then load the next chunk of each operand, compute the next chunk of the result, and store that, etc. Thus, even a processor which requires all additions and subtractions to go through a single 8-bit register can handle 32-bit signed numbers reasonably efficiently (slower than with a 32-bit register, of course, but still workable).
When using of the any other signed representations allowed by the C Standard, every bit of the result could potentially be affected by any bit of the operands, making it necessary to either hold an entire value in registers at once or else follow computations with an extra step that would, in at least some cases, require reading, modifying, and rewriting each chunk of the result.
There are different types of representations those are:
-Unsigned number representation used to represent only positive numbers
-Signed number representation used to represent positive as well as a negative number. In Signed number representation MSB bit represents sign bit and rest bits represents the number. When MSB is 0 means number is positive and When MSB is 1 means number is negative.
Problem with Signed number representation is that there are two values for 0.
Problem with one's complement representation is that there are two values for 0.
But if we use Two's complement representation then there will only one value for 0 that's why we represent negative numbers in two's complement form.
Source:Why negative numbers are stored in two's complement form bytesofgigabytes
We perform only addition operation for both addition and subtraction. We add the second operand to the first operand for addition. For subtraction we add the 2's complement of the second operand to the first operand.
With a 2's complement representation we do not need separate digital components for subtraction—only adders and complementers are used.
One satisfactory answer of why Two2's Complement is used to represent negative numbers rather than One's Complement system is that Two's Complement system solves the problem of multiple representations of 0 and the need for end-around-carry which exist in the One's complement system of representing negative numbers.
For more information Visit https://en.wikipedia.org/wiki/Signed_number_representations
For End-around-carry Visit https://en.wikipedia.org/wiki/End-around_carry
