Checking if two cubic Bézier curves intersect

Question

For a personal project, I'd need to find out if two cubic Bézier curves intersect. I don't need to know where: I just need to know if they do. However, I'd need to do it fast.

I've been scavenging the place and I found several resources. Mostly, there's this question here that had a promising answer.

So after I figured what is a Sylvester matrix, what is a determinant, what is a resultant and why it's useful, I thought I figured how the solution works. However, reality begs to differ, and it doesn't work so well.

---

Messing Around

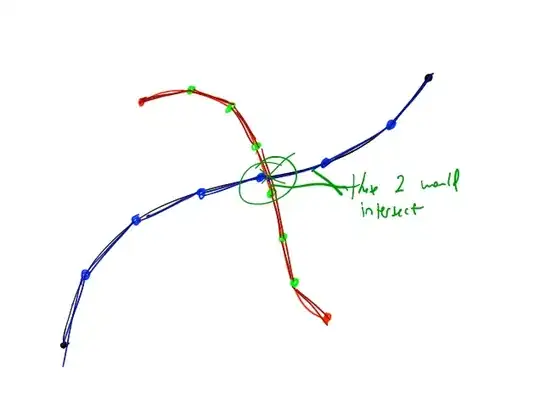
I've used my graphing calculator to draw two Bézier splines (that we'll call B₀ and B₁) that intersect. Their coordinates are as follow (P₀, P₁, P₂, P₃):

(1, 1) (2, 4) (3, 4) (4, 3)
(3, 5) (3, 6) (0, 1) (3, 1)

The result is the following, B₀ being the "horizontal" curve and B₁ the other one:

Following directions from the aforementioned question's top-voted answer, I've subtracted B₀ to B₁. It left me with two equations (the X and the Y axes) that, according to my calculator, are:

x = 9t^3 - 9t^2 - 3t + 2
y = 9t^3 - 9t^2 - 6t + 4

---

The Sylvester Matrix

And from that I've built the following Sylvester matrix:

9  -9  -3   2   0   0
0   9  -9  -3   2   0
0   0   9  -9  -3   2
9  -9  -6   4   0   0
0   9  -9  -6   4   0
0   0   9  -9  -6   4

After that, I've made a C++ function to calculate determinants of matrices using Laplace expansion:

template<int size>
float determinant(float* matrix)
{
    float total = 0;
    float sign = 1;
    float temporaryMatrix[(size - 1) * (size - 1)];
    for (int i = 0; i < size; i++)
    {
        if (matrix[i] != 0)
        {
            for (int j = 1; j < size; j++)
            {
                float* targetOffset = temporaryMatrix + (j - 1) * (size - 1);
                float* sourceOffset = matrix + j * size;
                int firstCopySize = i * sizeof *matrix;
                int secondCopySize = (size - i - 1) * sizeof *matrix;
                memcpy(targetOffset, sourceOffset, firstCopySize);
                memcpy(targetOffset + i, sourceOffset + i + 1, secondCopySize);
            }
            float subdeterminant = determinant<size - 1>(temporaryMatrix);
            total += matrix[i] * subdeterminant * sign;
        }
        sign *= -1;
    }
    return total;
}

template<>
float determinant<1>(float* matrix)
{
    return matrix[0];
}

It seems to work pretty well on relatively small matrices (2x2, 3x3 and 4x4), so I'd expect it to work on 6x6 matrices too. I didn't conduct extensive tests however, and there's a possibility that it's broken.

---

The Problem

If I understood correctly the answer from the other question, the determinant should be 0 since the curves intersect. However, feeding my program the Sylvester matrix I made above, it's -2916.

Is it a mistake on my end or on their end? What's the correct way to find out if two cubic Bézier curves intersect?

Answer 1

Intersection of Bezier curves is done by the (very cool) Asymptote vector graphics language: look for intersect() here.

Although they don't explain the algorithm they actually use there, except to say that it's from p. 137 of "The Metafont Book", it appears that the key to it is two important properties of Bezier curves (which are explained elsewhere on that site though I can't find the page right now):

• A Bezier curve is always contained within the bounding box defined by its 4 control points
• A Bezier curve can always be subdivided at an arbitrary t value into 2 sub-Bezier curves

With these two properties and an algorithm for intersecting polygons, you can recurse to arbitrary precision:

bezInt(B₁, B₂):

2. Does bbox(B₁) intersect bbox(B₂)?
   • No: Return false.
   • Yes: Continue.
3. Is area(bbox(B₁)) + area(bbox(B₂)) < threshold?
   • Yes: Return true.
   • No: Continue.
4. Split B₁ into B_1a and B_1b at t = 0.5
5. Split B₂ into B_2a and B_2b at t = 0.5
6. Return bezInt(B_1a, B_2a) || bezInt(B_1a, B_2b) || bezInt(B_1b, B_2a) || bezInt(B_1b, B_2b).

This will be fast if the curves don't intersect -- is that the usual case?

[EDIT] It looks like the algorithm for splitting a Bezier curve in two is called de Casteljau's algorithm.

Answer 2

If you're doing this for production code, I'd suggest the Bezier clipping algorithm. It's explained well in section 7.7 of this free online CAGD text (pdf), works for any degree of Bezier curve, and is fast and robust.

While using standard rootfinders or matrices might be more straightforward from a mathematical point of view, Bezier clipping is relatively easy to implement and debug, and will actually have less floating point error. This is because whenever it's creating new numbers, it's doing weighted averages (convex combinations) so there's no chance of extrapolating based on noisy inputs.

Answer 3

Is it a mistake on my end or on their end?

Are you basing your interpretation of the determinant on the 4th comment attached to this answer? If so, I believe that's where the mistake lies. Reproducing the comment here:

If the determinant is zero there is is a root in X and Y at *exactly the same value of t, so there is an intersection of the two curves. (the t may not be in the interval 0..1 though).

I don't see any problems with this part, but the author goes on to say:

If the determinant is <> zero you can be sure that the curves don't intersect anywhere.

I don't think that's correct. It's perfectly possible for the two curves to intersect in a location where the t values differ, and in that case, there will be an intersection even though the matrix has a non-zero determinant. I believe this is what's happening in your case.

Answer 4

This is a hard problem. I would split each of the 2 Bezier curves into say 5-10 discrete line segments, and just do line-line intersections.

foreach SampledLineSegment line1 in Bezier1
    foreach SampledLineSegment line2 in Bezier2
        if( line1 intersects line2 )
            then Bezier1 intersects Bezier2

Answer 5

I don't know how fast it will be, but if you have two curves C1(t) and C2(k) they intersect if C1(t) == C2(k). So you have two equations (per x and per y) for two variables (t, k). You can solve the system using numerical methods with enough for you accuracy. When you've found t,k parameters you should check if there is a parameter on [0, 1]. If it is they intersects on [0, 1].

Answer 6

I'm by no way an expert on this kind of thing, but I follow a nice blog that talks a lot about curves. He has link to two nice articles talking about your problem (the second link has an interactive demonstration and some source code). Other people may have much better insight into the problem but I hope this helps!

http://cagd.cs.byu.edu/~557/text/ch7.pdf (archived copy)

Answer 7

I would say that the easiest and likely fastest answer is to subdivide them into very small lines and find the points where the curves intersect, if they actually do.

public static void towardsCubic(double[] xy, double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3, double t) {
    double x, y;
    x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3;
    y = (1 - t) * (1 - t) * (1 - t) * y0 + 3 * (1 - t) * (1 - t) * t * y1 + 3 * (1 - t) * t * t * y2 + t * t * t * y3;
    xy[0] = x;
    xy[1] = y;
}

public static void towardsQuad(double[] xy, double x0, double y0, double x1, double y1, double x2, double y2, double t) {
    double x, y;
    x = (1 - t) * (1 - t) * x0 + 2 * (1 - t) * t * x1 + t * t * x2;
    y = (1 - t) * (1 - t) * y0 + 2 * (1 - t) * t * y1 + t * t * y2;
    xy[0] = x;
    xy[1] = y;
}

Obviously the brute force answer is bad See bo{4}'s answer, and there's a lot of linear geometry and collision detection that will actually help quite a lot.

---

Pick the number of slices you want for the curves. Something like 100 should be great.

We take all the segments and sort them based on the largest value of y they have. We then, add a second flag in the list for the smallest value of y for that segment.

We keep a list of active edges.

We iterate through the y-sorted list of segment, when we encounter a leading segment we add it to the active list. When we hit the small-y flagged value, we remove that segment from the active list.

We then can simply iterate through the entire set of segments with what amounts to a scan line, increasing our y monotonically as we simply iterate the list. We iterate through the values in our sorted list, which will typically remove one segment and add a new segment (or for split and merge nodes, add two segments or remove two segments). Thereby keeping an active list of relevant segments.

We run the fast fail intersect check as we add a new active segment to the list of active segments, against only that segment and and the currently active segments.

So at all times we know exactly which line segments are relevant, as we iterate through the sampled segments of our curves. We know these segments share overlap in the y-coords. We can fast fail any new segment that does not overlap with regard to its x-coords. In the rare case that they overlap in the x-coords, we then check if these segments intersect.

This will likely reduce the number of line intersection checks to basically the number of intersections.

foreach(segment in sortedSegmentList) {
    if (segment.isLeading()) {
        checkAgainstActives(segment);
        actives.add(segment);
    }
    else actives.remove(segment)
}

checkAgainstActive() would simply check if this segment and any segment in the active list overlap their x-coords, if they do, then run the line intersect check on them, and take the appropriate action.

---

Also note, this will work for any number of curves, any type of curves, any order of curves, in any mixture. And if we iterate through the entire list of segments it will find every intersection. It will find every point a Bezier intersects a circle or every intersection that a dozen quadratic Bezier curves have with each other (or themselves), and all in the same split second.

The oft cited Chapter 7 document notes, for the subdivision algorithm:

"Once a pair of curves has been subdivided enough that they can each be approximated by a line segment to within a tolerance"

We can literally just skip the middleman. We can do this fast enough so to simply compare line segments with a tolerable amount of error from the curve. In the end, that's what the typical answer does.

---

Secondly, note, that the bulk of the speed increase for the collision detection here, namely the ordered list of segments sorted based on their highest y to add to the active list, and lowest y to remove from the active list, can likewise be done for the hull polygons of the Bezier curve directly. Our line segment is simply a polygon of order 2, but we could do any number of points just as trivially, and checking the bounding box of all the control points in whatever order of curve we're dealing with. So rather than a list of active segments, we would have a list of active hull polygons points. We could simply use De Casteljau's algorithm to split the curves, thereby sampling as these as subdivided curves rather than line segments. So rather than 2 points we'd have 4 or 7 or whatnot, and run the same routine being quite apt towards fast failing.

Adding the relevant group of points at max y, removing it at min y, and comparing only the active list. We can thus quickly and better implement the Bezier subdivision algorithm. By simply finding bounding box overlap, and then subdividing those curves which overlapped, and removing those that did not. As, again, we can do any number of curves, even ones subdivided from curves in the previous iteration. And like our segment approximation quickly solve for every intersection position between hundreds of different curves (even of different orders) very quickly. Just check all curves to see if the bounding boxes overlap, if they do, we subdivide those, until our curves are small enough or we ran out of them.

Answer 8

Yes, I know, this thread is accepted and closed for a long time, but...

First, I'd like to thank you, zneak, for an inspiration. Your effort allows to find the right way.

Second, I was not quite happy with the accepted solution. This kind is used in my favorite freeware IPE, and its bugzilla is plenty of complains for a low accuracy and reliability about an intersection issue, my among them.

The missing trick which allows to solve the problem in a manner proposed by zneak : It is enough to shorten one of curves by a factor k>0, then the determinant of Sylvester matrix will be equal to zero. It is obvious, if a shortened curve will intersect, then original will too. Now, the task is changed into the search for a suitable value for k factor. This has led to the problem of solving an univariate polynomial of 9 degree. A real and positive roots of this polynomial are responsible for potential points of intersection. (This shouldn't be a surprise, two cubic Bezier curves can intersect up to 9 times.) The final selection is performed to find only those k factors, which provide 0<=t<=1 for both curves.

Now the Maxima code, where the starting point is set of 8 points provided by zneak :

p0x:1; p0y:1;
p1x:2; p1y:4;
p2x:3; p2y:4;
p3x:4; p3y:3;

q0x:3; q0y:5;
q1x:3; q1y:6;
q2x:0; q2y:1;
q3x:3; q3y:1;

c0x:p0x;
c0y:p0y;
c1x:3*(p1x-p0x);
c1y:3*(p1y-p0y);
c2x:3*(p2x+p0x)-6*p1x;
c2y:3*(p2y+p0y)-6*p1y;
c3x:3*(p1x-p2x)+p3x-p0x;
c3y:3*(p1y-p2y)+p3y-p0y;

d0x:q0x;
d0y:q0y;
d1x:3*(q1x-q0x);
d1y:3*(q1y-q0y);
d2x:3*(q2x+q0x)-6*q1x;
d2y:3*(q2y+q0y)-6*q1y;
d3x:3*(q1x-q2x)+q3x-q0x;
d3y:3*(q1y-q2y)+q3y-q0y;

x:c0x-d0x + (c1x-d1x*k)*t+ (c2x-d2x*k^2)*t^2+ (c3x-d3x*k^3)*t^3;
y:c0y-d0y + (c1y-d1y*k)*t+ (c2y-d2y*k^2)*t^2+ (c3y-d3y*k^3)*t^3;

z:resultant(x,y,t);

At this point, Maxima answered:

(%o35)−2*(1004*k^9−5049*k^8+5940*k^7−1689*k^6+10584*k^5−8235*k^4−2307*k^3+1026*k^2+108*k+76)

Let Maxima solve this equation:

rr: float( realroots(z,1e-20))  

The answer is:

(%o36) [k=−0.40256438624399,k=0.43261490325108,k=0.84718739982868,k=2.643321910825066,k=2.71772491293651]

Now the code to select a right value of k:

for item in rr do ( 
  evk:ev(k,item),
  if evk>0 then (  
    /*print("k=",evk),*/ 
    xx:ev(x,item),  rx:float( realroots(xx,1e-20)),/*print("x(t)=",xx,"   roots: ",rx),*/
    yy:ev(y,item),  ry:float( realroots(yy,1e-20)),/*print("y(t)=",yy,"   roots: ",ry),*/
    for it1 in rx do (  t1:ev(t,it1),
    for it2 in ry do (  t2:ev(t,it2),
       dt:abs(t1-t2),
       if dt<1e-10 then (
         /*print("Common root=",t1,"  delta t=",dt),*/
         if (t1>0) and (t1<=1) then ( t2:t1*evk,
         if (t2>0) and (t2<=1) then (                           
                 x1:c0x + c1x*t1+ c2x*t1^2+ c3x*t1^3,
                 y1:c0y + c1y*t1+ c2y*t1^2+ c3y*t1^3,
                 print("Intersection point:     x=",x1, "      y=",y1)
)))))/*,disp ("-----")*/
));

Maxima's answer:

"Intersection point:     x="1.693201254437358"      y="2.62375005067273
(%o37) done

Theres not only a honey, though. The presented method is unusable, if:

• P0=Q0, or more generally, if P0 lies on the second curve (or its extension). One can try to swap the curves.
• an extremely rare cases, when both curves belong to one K-family (eg. their infinite extensions are the same).
• keep an eyes on (sqr(c3x)+sqr(c3y))=0 or (sqr(d3x)+sqr(3y))=0 cases, here a quadratic are pretending to be a cubic Bezier curves.

One can ask, why a shortening is performed only once. It's enough because of reverse-inverse law, which was discovered en passant, but this is an another story.