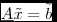Geo-Search (Distance) in PHP/MySQL (Performance)

Question

I have a MySQL-table (MyISAM) containing about 200k entries of lat/long pairs that I select from, based on the pairs distance (great circle formula) from another lat/long pair. (e.g. all entries that are within a 10km radius around 50.281852, 2.504883)

My problem is that this query takes about 0,28 sec. to run just for those 200k entries (which continue to get more every day). While 0,28 sec. would be fine normally, this query runs very often as it powers the main feature of my web-app, and often times it's part of a larger query.

Is there any way to speed this up? Obviously MySQL has to run through all 200k entries every time and perform the great circle formula for every entry. I read something about geohashing, R-Trees and the like here on Stack Overflow but I don't think that's the way I want to go. Partly because I've never been a big fan of maths, but mostly because I think that this problem has already been solved by someone smarter than me in a library/extension/etc. that has been tested extensively and is being updated regularly.

MySQL seems to have a spatial extension but that one doesn't provide a distance function. Should I be looking at another database to put this coordinate-pairs in? PostgreSQL seems to have a fairly mature Spatial extension. Do you know anything about it? Or would PostgreSQL too simply just use the great circle formula to get all entries within a certain region?

Is there maybe a specialized stand-alone product or mysql-extension that already does what I'm looking for?

Or is there maybe A PHP library I could use to do the calculations? Using APC I could easily fit the lat-long pairs into memory (those 200k entries take about 5MB) and then run the query inside of PHP. The problem with this approach however is that then I'd have a MySQL query like SELECT .. FROM .. WHERE id in (id1, id2, ..) for all the results which can be up to a few thousand. How well does MySQL handle Queries like these? And then (since this is a number-crunching task) would doing this in PHP be fast enough?

Any other Ideas what I should/shouldn't do?

For completeness, here is the sample query, stripped of any irrelevant parts (as I said, usually this is part of a bigger query where I join multiple tables):

SELECT id,
       6371 * acos( sin( radians( 52.4042924 ) ) * sin( radians( lat ) ) + cos( radians( 50.281852 ) ) * cos( radians( lat ) ) * cos( radians( 2.504883 ) - radians( lon ) ) ) AS dst
FROM geoloc
HAVING dst <10
ORDER BY dst ASC

Answer 1

What if you approach the problem from a different angle?

10 km in a straight line is:

1. on the latitude is equal to ~1'(minute)
2. on the longitude is equal to ~6'(minutes)

Using this as a basis, do some quick math and in your query add to the WHERE clause removing any locations that are outside the 'box' that is created by adding the buffer zone with the assumption of 1' lat & 6' long

Working from this image:

1. GPS location you are searching for (34° 12' 34.0", -85° 1' 1.0") [34.2094444444, -85.0169444444]

2. You find the min/max latitude/longitude

   2a. Min Latitude - 34.1927777778, -85.0169444444

   2b. Min Longitude - 34.2094444444, -85.1169444444

   2c. Max Latitude - 34.2261111111, -85.0169444444

   2d. Max Longitude - 34.2094444444, -84.9169444444

3. Run your query with the min and max of each direction

   SELECT *
   
   FROM geoloc
   
   WHERE
   
   lat >= 34.1927777 AND
   
   lat <= 34.2261111 AND
   
   long >= -85.1169444 AND
   
   long <= -84.9169444;
   

You can either integrate the distance calculation with the SQL query or you can use a PHP library/class to run the distance check after pulling the data. Either way you have reduced the number of calculations by a large percentage.

I use the following function to calculate the distance between two US84 GPS locations. Two parameters are passed, each parameter is an array with the first element being the latitude and the second element being the longitude. I believe it has an accuracy to a few feet, which should be enough for all but the hardest core GPS-ophiles. Also, I believe this uses the Haversine distance formula.

$distance = calculateGPSDistance(array(34.32343, -86.342343), array(34.433223, -96.0032344));

function calculateGPSDistance($site1, $site2)
{
    $distance = 0;
    $earthMeanRadius = 2.0891 * pow(10, 7);

    $deltaLatitude = deg2rad($site2[0] - $site1[0]);
    $deltaLongitude = deg2rad($site2[1] - $site1[1]);
    $a = sin($deltaLatitude / 2) * sin($deltaLatitude / 2) + cos(deg2rad($site1[0])) * 
        cos(deg2rad($site2[0])) * sin($deltaLongitude / 2) * sin($deltaLongitude / 2);
    $c = 2 * atan2(sqrt($a), sqrt(1-$a));
    $distance = $earthMeanRadius * $c;

    return $distance;
}

UPDATE

I forgot to mention, my distance function will return distance in feet.

Answer 2

Calculate a bounding box to select a subset of the rows in the WHERE clause of your SQL query, so that you're only executing the expensive distance calculation on that subset of rows rather than against the entire 200k records in your table. The method is described in this article on Movable Type (with PHP code examples). Then you can include the Haversine calculation in your query against that subset to calculate the actual distances, and factor in the HAVING clause at that point.

It's the bounding box that helps your performance, because it means you're only doing the expensive distance calculation on a small subset of your data. This is effectively the same method that Patrick has suggested, but the Movable Type link has extensive explanations of the method, as well as PHP code that you can use to build the bounding box and your SQL query.

EDIT

If you don't think haversine is accurate enough, then there's also the Vincenty formula.

//  Vincenty formula to calculate great circle distance between 2 locations expressed as Lat/Long in KM

function VincentyDistance($lat1,$lat2,$lon1,$lon2){
    $a = 6378137 - 21 * sin($lat1);
    $b = 6356752.3142;
    $f = 1/298.257223563;

    $p1_lat = $lat1/57.29577951;
    $p2_lat = $lat2/57.29577951;
    $p1_lon = $lon1/57.29577951;
    $p2_lon = $lon2/57.29577951;

    $L = $p2_lon - $p1_lon;

    $U1 = atan((1-$f) * tan($p1_lat));
    $U2 = atan((1-$f) * tan($p2_lat));

    $sinU1 = sin($U1);
    $cosU1 = cos($U1);
    $sinU2 = sin($U2);
    $cosU2 = cos($U2);

    $lambda = $L;
    $lambdaP = 2*M_PI;
    $iterLimit = 20;

    while(abs($lambda-$lambdaP) > 1e-12 && $iterLimit>0) {
        $sinLambda = sin($lambda);
        $cosLambda = cos($lambda);
        $sinSigma = sqrt(($cosU2*$sinLambda) * ($cosU2*$sinLambda) + ($cosU1*$sinU2-$sinU1*$cosU2*$cosLambda) * ($cosU1*$sinU2-$sinU1*$cosU2*$cosLambda));

        //if ($sinSigma==0){return 0;}  // co-incident points
        $cosSigma = $sinU1*$sinU2 + $cosU1*$cosU2*$cosLambda;
        $sigma = atan2($sinSigma, $cosSigma);
        $alpha = asin($cosU1 * $cosU2 * $sinLambda / $sinSigma);
        $cosSqAlpha = cos($alpha) * cos($alpha);
        $cos2SigmaM = $cosSigma - 2*$sinU1*$sinU2/$cosSqAlpha;
        $C = $f/16*$cosSqAlpha*(4+$f*(4-3*$cosSqAlpha));
        $lambdaP = $lambda;
        $lambda = $L + (1-$C) * $f * sin($alpha) * ($sigma + $C*$sinSigma*($cos2SigmaM+$C*$cosSigma*(-1+2*$cos2SigmaM*$cos2SigmaM)));
    }

    $uSq = $cosSqAlpha*($a*$a-$b*$b)/($b*$b);
    $A = 1 + $uSq/16384*(4096+$uSq*(-768+$uSq*(320-175*$uSq)));
    $B = $uSq/1024 * (256+$uSq*(-128+$uSq*(74-47*$uSq)));

    $deltaSigma = $B*$sinSigma*($cos2SigmaM+$B/4*($cosSigma*(-1+2*$cos2SigmaM*$cos2SigmaM)- $B/6*$cos2SigmaM*(-3+4*$sinSigma*$sinSigma)*(-3+4*$cos2SigmaM*$cos2SigmaM)));

    $s = $b*$A*($sigma-$deltaSigma);
    return $s/1000;
}


echo VincentyDistance($lat1,$lat2,$lon1,$lon2);

Answer 3

What I was doing till now is just as @Mark described above. A viable solution for small sites I guess, only not that good for my case (200k entries localized inside some 100x100 square km box centered around a given point. I was using this same trick of Mark's but performance is just too poor. 5 users/second querying for nearby lat/lon points for few hours and the queries start taking up to 10 - 15 seconds; and this happens after I have adjusted mySQL settings in my.cnf. Don't even want to think about what would happen when there will be 2 million entries worldwide.

So, now time for step 2: Hilbert curve. It should solve the problem of B-tree index on (lat, lon) columns which is wasteful (onrange scans, ony one part of the B-tree index is being used) by employing just one index on one column (hilbert_number). hilbert_number being a number calculated based on a point's lat/lon coordinates on the Hilbert curve.

But the second problem, of testing the distance between fixed point and everything from the previous result subset through the Haversine formula remains. That part can be very slow. So I was thinking about somehow testing for distance more directly, putting everything on the hilbert curve and applying some bitmask to that result subset instead of applying the Haversine formula. I just don't know how would I go about that...

Anyway, another trick I have employed to reduce the number of points in the result subset was to use two bounding boxes and include in the subset only the gray / white points for further Haversine testing:

What I need to do right now is switch to Hilbert numbers and see how it behaves. But I doubt this is going to increase 10x the performance!

Answer 4

You could try a quadkey. It's a spatial index and reduce the dimension. It subdivide a map into tiles but you can use it to store points. You can download my php class hilbert-curve @ phpclasses.org. It also includes a z-curve and a moore-curve. Important is to know it uses a mercator projection. You can look for Bing maps tiling. It explains how to use a quadkey. You need x,y coordinate and z (zoom or depth) value. Then it gives you a quadkey.