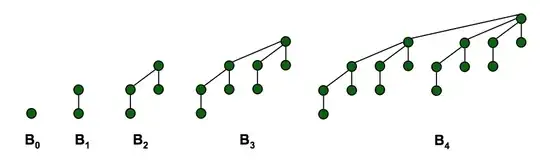
The key difference between a binary heap and a binomial heap is how the heaps are structured. In a binary heap, the heap is a single tree, which is a complete binary tree. In a binomial heap, the heap is a collection of smaller trees (that is, a forest of trees), each of which is a binomial tree. A complete binary tree can be built to hold any number of elements, but the number of elements in a binomial tree of some order n is always 2n. Consequently, we only need one complete binary tree to back a binary heap, but we may need multiple binomial trees to back a binomial heap. Interestingly, the orders of the binomial trees used in a binomial heap correspond to the 1 bits set in the binary representation of the number of elements in the forest.
The reason for organizing binomial heaps as they are is that a binomial tree of order n always has exactly 2n nodes in it. This allows us to make assumptions about the number of elements in the binomial tree without actually having to inspect the structure of that tree. On the other hand, a complete binary tree of some height h may have a variable number of nodes in it depending on how the last row is filled out. The fact that each of the children must have a very precisely-defined structure can also be used to prove that the number of children is at most O(log n), where n is the total number of nodes in the heap, which means that the cost of a delete-min is not too large.
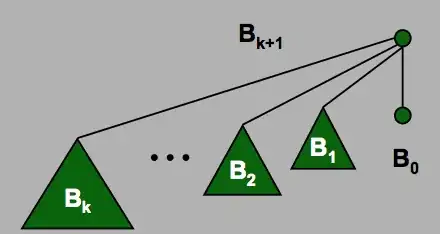
An important detail behind this is that a binomial heap is not any tree that happens to have k children. It's a tree that's rigorously defined as
- The binomial tree of order 0 is a single node, and
- The binomial tree of order n is a single node with binomial trees of order 0, 1, 2, ..., n - 1 as children.
(Technically, the order 0 special case isn't necessary here). You can see this here:

Note that there is exactly one tree of each order, with no flexibility at all in the number or position of the nodes.
However, an important alternative definition is the following:
- The binomial tree of order 0 is a single node, and
- The binomial tree of order n is two binomial trees of order n - 1, with one of the trees made a child of the other.
(Take a minute to see why these are equivalent). Using this second definition, it's a quick induction proof to show that the number of nodes in the tree is 2n. As a base case, a tree of order 0 has 20 = 1 nodes as required. For the inductive step, if we have two trees of order n - 1, they collectively have 2n-1 + 2n-1 = 2n nodes as required. Thus the total number of nodes in a binomial tree of order n is exactly 2n.
The idea for a heap that you're describing in your final paragraph does not always lead to an efficient runtime. In particular, if you have trees with a huge branching factor and no other structural constraints, then you could in theory build a heap of n nodes consisting of a single node with (n - 1) children. In that case, after deleting the minimum element from the heap, you'd have to look at all n - 1 children to determine which was the new minimum, giving a runtime of O(n). The other structural constraints on trees like complete binary trees, binomial trees, etc. guarantee that this worst-case doesn't happen.
Hope this helps!