4

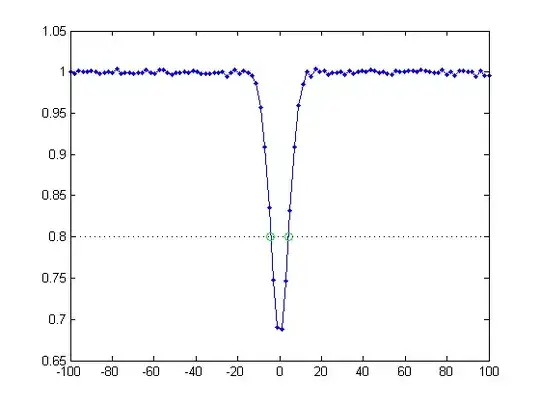
Here is the graph I currently have :

The Dotted Blue line represented the y value that corresponds to the x value I am looking for. I am trying to find the x values of the line's intersections with the blue curve(Upper)

The Dotted Blue line represented the y value that corresponds to the x value I am looking for. I am trying to find the x values of the line's intersections with the blue curve(Upper).Since the interesections do not fall on a point that has already been defined, we need to interpolate a point that falls onto the Upper plot.

Here is the information I have:

LineValue - The y value of the intersection and the value of the dotted line( y = LineValue) Frequency - an array containing the x value coordinates seen on this plot. The interpolated values of Frequency that corresponds to LineValue are what we are looking for Upper/Lower - arrays containing the y value info for this graph

Jonas Stein
  • 6,826
  • 7
  • 40
  • 72
Alex Nichols
  • 876
  • 5
  • 12
  • 23
  • possible duplicate of [matlab, how do i write a statement that will give me time on xaxis from y=0.3](http://stackoverflow.com/questions/5584873/matlab-how-do-i-write-a-statement-that-will-give-me-time-on-xaxis-from-y-0-3) – Amro Aug 04 '11 at 22:43

3 Answers3

8

This solution is an improvement on Amro's answer. Instead of using fzero you can simply calculate the intersection of the line by looking for transition in the first-difference of the series created by a logical comparison to LineValue. So, using Amro's sample data:

>> x = linspace(-100,100,100);
>> y =  1-2.*exp(-0.5*x.^2./20)./(2*pi) + randn(size(x))*0.002;
>> LineValue = 0.8;

Find the starting indices of those segments of consecutive points that exceed LineValue:

>> idx = find(diff(y >= LineValue))

idx =

    48    52

You can then calculate the x positions of the intersection points using weighted averages (i.e. linear interpolation):

>> x2 = x(idx) + (LineValue - y(idx)) .* (x(idx+1) - x(idx)) ./ (y(idx+1) - y(idx))

x2 =

         -4.24568579887939          4.28720287203057

Plot these up to verify the results:

>> figure;
>> plot(x, y, 'b.-', x2, LineValue, 'go', [x(1) x(end)], LineValue*[1 1], 'k:');

enter image description here

The advantages of this approach are:

  • The determination of the intersection points is vectorized so will work regardless of the number of intersection points.
  • Determining the intersection points arithmetically is presumably faster than using fzero.
Community
  • 1
  • 1
b3.
  • 7,094
  • 2
  • 33
  • 48
2

Example solution using FZERO:

%# data resembling your curve
x = linspace(-100,100,100);
f = @(x) 1-2.*exp(-0.5*x.^2./20)./(2*pi) + randn(size(x))*0.002;
VALUE = 0.8;

%# solve f(x)=VALUE
z1 = fzero(@(x)f(x)-VALUE, -10);  %# find solution near x=-10
z2 = fzero(@(x)f(x)-VALUE, 10);   %# find solution near x=+10

%# plot
plot(x,f(x),'b.-'), hold on
plot(z1, VALUE, 'go', z2, VALUE, 'go')
line(xlim(), [VALUE VALUE], 'Color',[0.4 0.4 0.4], 'LineStyle',':')
hold off

screenshot

Amro
  • 123,847
  • 25
  • 243
  • 454
0

Are the step sizes in your data series the same? Is the governing equation assumed to be cubic, sinuisoidal, etc..?

doc interpl Find the zero crossings

Jacob M
  • 1