Distance of wgs point from a wgs defined line segment

Question

I searched but I could not find a complete answer. In C# if at all possible. I need the shortest distance between a WGS point and a WGS point defined line segment on a sphere (Earth exactly).

float DistanceInKilometres(PointF LineStartA, PointF LineEndB, PointF ThePoint)

EDIT: Perhaps an illustration would help

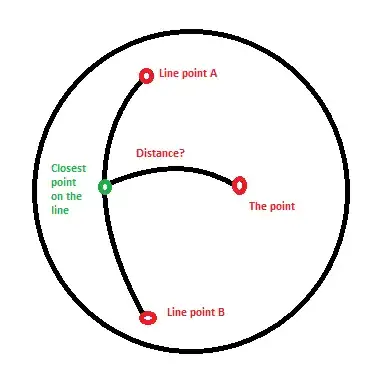
enter image description here

Please note that this is an ideal example. 'The point' could be anywhere on the surface of the sphere, the segment start-end, too. Obviously, I'm not looking for the distance through the sphere. Math isn't my stronger side, so I don't understand normalize or to cartesian. Maybe I should also note that path AB, is the shortest possible, and Distance?, is the shortest possible too.

I'm surprised that nobody has even a link to a possible solution? — JJ_Jason, Apr 06 '12 at 18:46
Related or duplicate: http://stackoverflow.com/questions/1299567/how-to-calculate-distance-from-a-point-to-a-line-segment-on-a-sphere — Nate Kohl, Apr 06 '12 at 20:25
@Nate Kohl And when I said 'I could not find a complete answer', that is what I meant. — JJ_Jason, Apr 06 '12 at 20:27
It might be worth further describing your constraints in your question -- i.e. it sounds like you *don't* want distance on a sphere, because there would be too much error? Were there other questions that were close, but fell short in some way? Etc. — Nate Kohl, Apr 06 '12 at 20:32
e.g. http://stackoverflow.com/questions/7803004/distance-from-point-to-line-on-earth — Nate Kohl, Apr 06 '12 at 20:34
The accepted question came very close(?), but i don'u understand what normalize, vectorProduct and toCartsian means in the accepted answer because it's in java or a mathematical expression, or both. I couldn't test it for the same reason. — JJ_Jason, Apr 06 '12 at 20:43
It might be a god idea to learn those things. Simple web searches should yeild a weath of information on the topic. — Sam Axe, Apr 06 '12 at 20:46

score 4 · Accepted Answer · edited May 23 '17 at 12:02

You can use the spherical law of cosines:

You will have to use the earth's radius for calculations:

EARTH_RADIUS_KM = 6371;

Here, from my contributions to OsmMercator.java, from openstreetmap.org:

/**
 * Gets the distance using Spherical law of cosines.
 *
 * @param la1 the Latitude in degrees
 * @param lo1 the Longitude in degrees
 * @param la2 the Latitude from 2nd coordinate in degrees
 * @param lo2 the Longitude from 2nd coordinate in degrees
 * @return the distance
 */
public static double getDistance(double la1, double lo1, double la2, double lo2) {
    double aStartLat = Math.toRadians(la1);
    double aStartLong = Math.toRadians(lo1);
    double aEndLat =Math.toRadians(la2);
    double aEndLong = Math.toRadians(lo2);

    double distance = Math.acos(Math.sin(aStartLat) * Math.sin(aEndLat)
            + Math.cos(aStartLat) * Math.cos(aEndLat)
            * Math.cos(aEndLong - aStartLong));

    return (EARTH_RADIUS_KM * distance);
}

All you need to do is find the closest point with dot product and use that with the distance equation.

Here's the closest point example:

double[] nearestPointSegment (double[] a, double[] b, double[] c)
{
   double[] t= nearestPointGreatCircle(a,b,c);
   if (onSegment(a,b,t))
     return t;
   return (distance(a,c) < distance(b,c)) ? a : c;
}

Keep in mind the units haven't been explicitly declared. When dealing with points in space there're are a variety of ways to determine position. The main thing is you have to nail down your units to a consistent type.

When working with position on the earth, I mainly use lat/long coordinates and vectors for magnitude/direction. There're are several known types to use for vectors and earth's position. Among them are the following:

Earth-centered earth-fixed (ECEF) coordinate system
North-East-Down (NED)
Geodetic coordinate system

For your example, I might consider sticking to Geodetic.

Now, bringing this together, you might have some pseudo code which looks like this:

Where a Vector is made up of Geodetic coordinates:
class Vector {
 double x=0.0; //latitude
 double y=0.0; //longitude
 double h=0.0; //height
...
}

public Vector closestPoint(Vector lineStartA, Vector lineEndB, final Vector thePoint ) {
    Vector w = thePoint.subtract(lineStartA);
    double proj = w.dot(lineEndB);
    // endpoint 0 is closest point
    if ( proj <= 0.0f )
        return lineStartA;
    else
    {
        //Vector square 
        double vsq = lineEndB.dot(lineEndB);
        // endpoint 1 is closest point
        if ( proj >= vsq )
            return lineStartA.add(lineEndB);
        else
            return lineStartA.add(lineEndB.multiply(proj/vsq));
    }
}      

double DistanceInKilometres(Vector lineStartA, Vector lineEndB, Vector thePoint) {
  Vector cp=closestPoint(lineStartA, lineEndB, thePoint);
  return getDistance(cp.x, cp.y, thePoint.x, thePoint.y);
}

Sry, got busy with work. I can't give my dot product code as it comes from our internal library. However, there are plenty suitable examples on the net. I think I have one bookmarked from past research. I'll check. — Jason Huntley, Apr 19 '12 at 19:13
Added the pseudo code for you. That should bring it together. — Jason Huntley, Apr 19 '12 at 20:00
'On segment' would be just comapring the north most and south most points with the latitude of thePoint? — JJ_Jason, Apr 20 '12 at 08:51
for which method? closest point? What are the values you're using as input? — Jason Huntley, Apr 20 '12 at 14:55
yes, closestPoint. I'm confused as to why are you using vectors as results? I suppose the return's value X,Y are lon,lat, respectively? — JJ_Jason, Apr 21 '12 at 09:27
@JJ_Jason I have the same problem. It always returns the vector `lineStartA`. Did you find a solution? — Daniel Kvist, Aug 07 '15 at 10:06

score 0 · Answer 2 · edited May 23 '17 at 10:32

0

If your point lies within a corridor that is defined by the end points of your line segment, and perpendicular to the line, then this answer should do.

If your point lies outside that corridor then compute the distance from your point to each end of the line segment and take the smaller.

edited May 23 '17 at 10:32

Community

1
1

answered Apr 06 '12 at 19:30

Sam Axe

33,313
9
55
89

That's not precise enough. Whether 'it lies' is relative. It is never exactly (or on a very rare occasion) 'on' the corridor. Even if it did, I do not know how to calculate that on a sphere, hence the question. For the second part, that's correct only, and only if the points longitude or latitude is the same as one of the line segment ends latitude or longitude. I'm afraid you misunderstood my question. – JJ_Jason Apr 06 '12 at 20:06
I believe you misread my answer. The second part has nothing to do with axial alignment. Distance would be near useless if the piint and the line had to be aligned on an axis. – Sam Axe Apr 06 '12 at 20:45
I get it now. The 'corridor' is actually a west-east corridor with it's north-most point being my 'Line point a' and south-most point being my 'Line point B'. Again, as posted in the answer, ' Does the same solution work for geographical points'? How to know if it is inside the corridor? – JJ_Jason Apr 06 '12 at 20:53
A simpler method would be to use the method from the answer, then compute the two end point distances.. take the smaller of the three. But the easiest solution is the one that Nate Kohl mentions in his comment. @Nate: I would encourage you to turn that comment into an answer. – Sam Axe Apr 06 '12 at 23:10

Distance of wgs point from a wgs defined line segment

2 Answers2

Linked