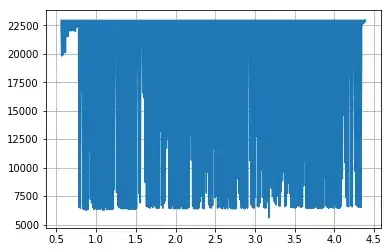
I've written some quick python code that will extract chromatogram (or any single-valued) data from an image file.
It has the following requirements:
- Image is clean (no text or other data).
- Curve is single valued, ie. curve pixel width of one (it will still work without this, but it will always take the upper value).
- Scales are linear.
It is very simple, and just iterates through each column of the image and takes the first black value as the data point. It uses PIL. These data points are initially in the image co-ordinate system, so need to be rescaled to the data co-ordinate system, if all your images share the same axis, this is straight forward, otherwise it needs to be done manually on a per image basis (automation would be more involved).
The image below shows where I extracted your image (I removed the text) for processing (non-pink region), so for re-scaling we just take the white box region in the data co-ordinate system: x_range = 4.4 - 0.55, x_offset = 0.55, y_range = 23000 - 2500, and y_offset = 2500.
Here is the extracted data replotted with pyplot:
Here is the code:
import Image
import numpy as np
def get_data(im, x_range, x_offset, y_range, y_offset):
x_data = np.array([])
y_data = np.array([])
width, height = im.size
im = im.convert('1')
for x in xrange(width):
for y in xrange(height):
if im.getpixel((x, y)) == 0:
x_data = np.append(x_data, x)
y_data = np.append(y_data, height - y)
break
x_data = (x_data / width) * x_range + x_offset
y_data = (y_data / height) * y_range + y_offset
return x_data, y_data
im = Image.open('clean_data_2.png')
x_data, y_data = get_data(im,4.4-0.55,0.55,23000-2500,2500)
from pylab import *
plot(x_data, y_data)
grid(True)
savefig('new_data.png')
show()
Once you have your data as numpy arrays, there are many options you can use to find peaks and the corresponding areas under them (see this discussion for some approaches). Noise is a large concern, so a general approach would be to convolve the data to smooth the noise out (or you could threshold if your peaks are sharp) then differentiate to find peaks. To find areas under peaks you can do numerical integration across the peak region.
I've made a couple of assumptions and written some simple code (below), to illustrate a possible approach. I've thresholded the data so only peaks above 5000 survive, then we iterate through the data finding the peaks, and using the trapeze rule, np.trapz, to find the area under each peak. Where peaks overlap the areas are split at the overlap point (I doubt this is standard..). Also this code will only recognize peaks that are local maxima (shoulders will not be detected). I've graphed the results, writing the area values for each peak at the corresponding peak position:
def find_peak(start, grad):
for index, gr in enumerate(grad[start:]):
if gr < 0:
return index + start
def find_end(peak, grad):
for index, gr in enumerate(grad[peak:]):
if gr >= 0:
return index + peak + 1
def find_peaks(grad):
peaks=[]
i = 0
while i < len(grad[:-1]):
if grad[i] > 0:
start = i
peak_index = find_peak(start, grad)
end = find_end(peak_index, grad)
area = np.trapz(y_data[start:end], x_data[start:end])
peaks.append((x_data[peak_index], y_data[peak_index], area))
i = end - 1
else:
i+=1
return peaks
y_data = np.where(y_data > 5000, y_data, 0)
grad = np.diff(y_data)
peaks = find_peaks(grad)
from pylab import *
plot(x_data, y_data)
for peak in peaks:
text(peak[0], 1.01*peak[1], '%d'%int(peak[2]))
grid(True)
show()
Whatever approach you take at this point requires assumptions about your data (which I am not really in a position to make! Although I made a few above!), how do you deal with overlapping peaks? etc.. I am sure there are standard approaches in chromatography, so really you need to check that out first. Hope this helps!