triggering an event with a certain probability with C#

Question

I'm trying to simulate a realistic key press event. For that reason I'm using SendInput() method, but for greater result I need to specify the delay between keyDOWN and KeyUP events! These numbers below show the elapsed time in milliseconds between DOWN and UP events (these are real/valid):

96 95 112 111 119 104 143 96 95 104 120 112 111 88 104 119 111 103 95 104 95 127 112 143 144 142 143 128 144 112 111 112 120 128 111 135 118 147 96 135 103 64 64 87 79 112 88 111 111 112 111 104 87 95

We can simplify the output:

delay 64 - 88 ms -> 20% of a time

delay 89 - 135 ms -> 60% of a time

delay 136 - 150 ms -> 20 % of a time

How do I trigger an event according to probabilities from above? Here is the code I'm using right now:

        private void button2_Click(object sender, EventArgs e)
        {
            textBox2.Focus();
            Random r = new Random();
            int rez = r.Next(0, 5); // 0,1,2,3,4 - five numbers total

            if (rez == 0) // if 20% (1/5)
            {
                Random r2 = new Random();
                textBox2.AppendText(" " + rez + " " + r2.Next(64, 88) + Environment.NewLine);
// do stuff
            }
            else if (rez == 4)//if 20% (1/5)
            {
                Random r3 = new Random();
                textBox2.AppendText(" " + rez + " " + r3.Next(89, 135) + Environment.NewLine);
// do stuff

            }
            else // if 1 or 2 or 3 (3/5) -> 60%
            {
                Random r4 = new Random();
                textBox2.AppendText(" " + rez + " " + r4.Next(136, 150) + Environment.NewLine);
// do stuff

            }

        }

There is a huge problem with this code. In theory, after millions of iterations - the resulting graph will look similar to this:

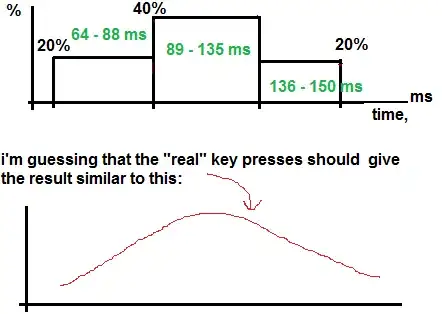
How to deal with this problem?

EDIT: the solution was to use distribution as people suggested.

here is java implementation of such code:

http://docs.oracle.com/javase/1.4.2/docs/api/java/util/Random.html#nextGaussian%28%29

and here is C# implementation:

How to generate normally distributed random from an integer range?

although I'd suggest to decrease the value of "deviations" a little.

here is interesting msdn article

http://blogs.msdn.com/b/ericlippert/archive/2012/02/21/generating-random-non-uniform-data-in-c.aspx

everyone thanks for help!

Answer 1

This is the right idea, I just think you need to use doubles instead of ints so you can partition the probability space between 0 and 1. This will allow you to get a finer grain, as follows :

1. Normalise the real values by dividing all the values by the largest value
2. Divide the values into buckets - the more buckets, the closer the graph will be to the continuous case
3. Now, the larger the bucket the more chance of the event being raised. So, partition the interval [0,1] according to how many elements are in each bucket. So, if you have 20 real values, and a bucket has 5 values in it, it takes up a quarter of the interval.
4. On each test, generate a random number between 0-1 using Random.NextDouble() and whichever bucket the random number falls into, raise an event with that parameter. So for the numbers you provided, here are the values for 5 buckets buckets :

This is a bit much to put in a code example, but hopefully this gives the right idea

Answer 2

Sounds like you need to generate a normal distribution. The built-in .NET class generates a Uniform Distribution.

Gaussian or Normal distribution random numbers are possible using the built-in Random class by using the Box-Muller transform.

You should end up with a nice probability curve like this

(taken from http://en.wikipedia.org/wiki/Normal_distribution)

To transform a Normally Distributed random number into an integer range, the Box-Muller transform can help with this again. See this previous question and answer which describes the process and links to the mathematical proof.

Answer 3

One possible approach would be to model the delays as an Exponential Distribution. The exponential distribution models the time between events that occur continuously and independently at a constant average rate - which sounds like a fair assumption given your problem.

You can estimate the parameter lambda by taking the inverse of the average of your real observed delays, and simulate the distribution using this approach, i.e.

delay = -Math.Log(random.NextDouble()) / lambda

However, looking at your sample, the data looks too "concentrated" around the mean to be a pure Exponential, so simulating that way would result in delays with the proper mean, but too spread out to match your sample.

One way to address that is to model the process as a shifted Exponential; essentially, the process is shifted by a value which represents the minimum the value can take, instead of 0 for an exponential. In code, taking the shift as the minimum observed value from your sample, this could look like this:

var sample = new List<double>()
                  {
                     96,
                     95,
                     112,
                     111,
                     119,
                     104,
                     143,
                     96,
                     95,
                     104,
                     120,
                     112
                  };

var min = sample.Min();
sample = sample.Select(it => it - min).ToList();

var lambda = 1d / sample.Average();

var random = new Random();
var result = new List<double>();
for (var i = 0; i < 100; i++)
{
   var simulated = min - Math.Log(random.NextDouble()) / lambda;
   result.Add(simulated);
   Console.WriteLine(simulated);
}

A trivial alternative, which is in essence similar to Aidan's approach, is to re-sample: pick random elements from your original sample, and the result will have exactly the desired distribution:

var sample = new List<double>()
                  {
                     96,
                     95,
                     112,
                     111,
                     119,
                     104,
                     143,
                     96,
                     95,
                     104,
                     120,
                     112
                  };

var random = new Random();
var size = sample.Count();
for (var i = 0; i < 100; i++)
{
   Console.WriteLine(sample[random.Next(0, size)]);
}