8

Recently I've been thinking about how to transform a complex polygon into a non-complex polygon. How is this done?

This is the sort of thing I want to do:

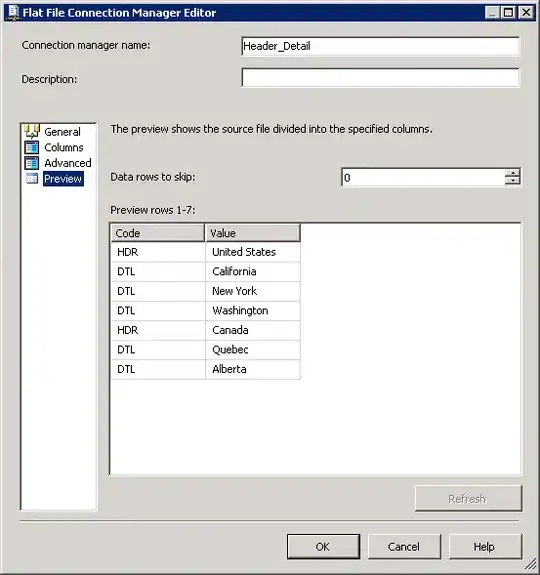
Example

I'm going to end up with JavaScript when I'm done, but any form of a solution is fine (language, algorithm, or just plain English).

Michael Petrotta
  • 59,888
  • 27
  • 145
  • 179

6 Answers6

6

I would use the same heuristic that I would use when drawing the polygon by hand (which is probably not the most mathematically efficient way to caluclaute that polygon, but probably the easiest to understand/implement).

  1. Start at a point
  2. Find all the intersections between my current point and the point I'm trying to get to
  3. If none exist draw to the next point
  4. If one does, then draw to there, and then set the next point to the next point from there
  5. If you aren't back to the beginning then goto 2.

Here is an example implementation on jsfiddle. Note: it isn't optimized.

J. Holmes
  • 18,466
  • 5
  • 47
  • 52
  • there aren't _two_ polygons - it's one polygon that's self-intersecting! – Alnitak May 20 '12 at 12:53
  • @Alnitak the same premise applies to a single self-intersecting polygon -- its actually simpler. – J. Holmes May 22 '12 at 01:29
  • +1 for the fiddle - just one question - what does the number 0.1 in `if (len > 0.1 && ...)` represent? – Alnitak May 22 '12 at 06:47
  • It's a pretty poorly designed check to make sure the intersections don't happen at segment end points – J. Holmes May 22 '12 at 12:55
  • yeah, I figured something like that. I was slightly concerned about "magic numbers" appearing in the algorithm. – Alnitak May 22 '12 at 12:56
  • It's not an algorithm, just a heuristic, it will only work on a certain type of complex polygons. But hopefully you glean something useful from it. – J. Holmes May 22 '12 at 12:57
  • This is actually a very nice solution. Another way is very similar to what you have here, but rather than automatically choosing a new direction after an intersection, first see if a closed point (e.g. midpoint) on the segment beyond the intersection is inside the overall shape, if not, then keep going in the same direction. [Winding number algorithm](http://geomalgorithms.com/a03-_inclusion.html) is easy enough to use for that purpose. That would work in (at least) two main cases that I'm aware of including the above example, though likely not on degenerate polygons or regions. – Nolo Jun 11 '16 at 07:13
3

I believe the easiest route is to perform a plane sweep to detect all the edge-edge intersections. It is not difficult to augment a basic plane-sweep algorithm implementation to maintain the outermost boundary, which is what you want. Almost every textbook on computational geometry explains this well.

Joseph O'Rourke
  • 4,346
  • 16
  • 25
2

This is a late answer, but this can be done using Javascript Clipper Library. The desired operation is Simplifying (which internally uses Union operation) and it removes self-intersections where edge(s) crosses other edge(s).

Note! Javascript Clipper 5 cannot ensure that in all cases the solution consists only of truly simple polygons. This like special case is the vertices touching edges. Clipper 6 (Javascript version not yet ready) can handle these like special cases also.

Simplifying Polygons using Javascript Clipper Main Demo

You can play with Clipper using Javascript Clipper Main Demo. Click Polygons-Custom and you can input your own polygon there and then make the desired operations.

Let's take your example:
[[7,86, 196,24, 199,177, 47,169, 51,21, 224,102, 223,146, 7,140, 7,86]]

If you input these points in demo (as Subject or Clip), you get the following polygon: enter image description here

Then make a Simplify operation which produces the following solution:

enter image description here

If you click Solution in Polygon Explorer, you can see the coordinates of simplified polygon: [[199,177, 47,169, 47.75,141.13, 7,140, 7,86, 49.62,72.02, 51,21, 114.51,50.73, 196,24, 197.28,89.49, 224,102, 223,146, 198.38,145.32]]

Code example of Simplifying Polygons

And finally, I put the full functional code in JSBIN, which includes SVG drawing functions and is therefore rather long:

<html>
  <head>
    <title>Javascript Clipper Library / Simplifying Polygons</title>
    <script src="clipper.js"></script>
    <script>
function draw() {
  var subj_polygons = [[{"X":7,"Y":86},{"X":196,"Y":24},{"X":199,"Y":177},{"X":47,"Y":169},{"X":51,"Y":21},{"X":224,"Y":102},{"X":223,"Y":146},{"X":7,"Y":140},{"X":7,"Y":86}]];
  var scale = 100;
  subj_polygons = scaleup(subj_polygons, scale);
  var cpr = new ClipperLib.Clipper();
  cpr.AddPolygons(subj_polygons, ClipperLib.PolyType.ptSubject);

  var solution_polygons = new ClipperLib.Polygons();
solution_polygons = cpr.SimplifyPolygons(subj_polygons, ClipperLib.PolyFillType.pftNonZero);
  //console.log(JSON.stringify(solution_polygons));
  var svg = '<svg style="margin-top:10px; margin-right:10px;margin-bottom:10px;background-color:#dddddd" width="240" height="200">';
  svg += '<path stroke="black" fill="yellow" stroke-width="2" d="' + polys2path(solution_polygons, scale) + '"/>';
  svg += '</svg>';
  document.getElementById('svgcontainer').innerHTML = svg;
}

// helper function to scale up polygon coordinates
function scaleup(poly, scale) {
  var i, j;
  if (!scale) scale = 1;
  for(i = 0; i < poly.length; i++) {
    for(j = 0; j < poly[i].length; j++) {
      poly[i][j].X *= scale;
      poly[i][j].Y *= scale;
    }
  }
  return poly;
}

// converts polygons to SVG path string
function polys2path (poly, scale) {
  var path = "", i, j;
  if (!scale) scale = 1;
  for(i = 0; i < poly.length; i++) {
    for(j = 0; j < poly[i].length; j++) {
      if (!j) path += "M";
      else path += "L";
      path += (poly[i][j].X / scale) + ", " + (poly[i][j].Y / scale);
    }
    path += "Z";
  }
  return path;
}
    </script>
  </head>
  <body onload="draw()">
  <h2>Javascript Clipper Library / Simplifying Polygons</h2>
  This page shows an example of simplifying polygon and drawing it using SVG.
    <div id="svgcontainer"></div>
  </body>
</html>
Timo Kähkönen
  • 11,962
  • 9
  • 71
  • 112
1

You should maintain list of incident edges for every intersection point.

Then for ever point choose edge (outgoing), which has the smallest angle (anti-clockwise) with the previous (incoming) edge.

MBo
  • 77,366
  • 5
  • 53
  • 86
  • 2
    "First, catch your wild boar." *(19th-century recipe)* Getting intersection points is not particularly straightforward, let alone maintaining a list of edges and external vertices. – Andrew Leach May 20 '12 at 14:00
  • @AndrewLeach Why getting intersection points is "not particularly straightforward"? Checking if two segments intersect is relatively simple (not mentioning that resources are widely available online) and it pretty much solves the problem. Yes, optimal solution is hard, but who says it have to be optimal? – zduny May 20 '12 at 14:21
  • @Andrew Leach There are some problems under determining external contour of complex polygons union or self-intersecting polygon - self-touching, precision issues, treatment of internal contours etc/ But getting intersection points and traversal external ones seems rather simple task (must admit that I've lack of experience with self-intersecting polygons) – MBo May 20 '12 at 16:42
0

It seems like you're going to want to look into Convex Hull algorithms. Here's an applet of a few Convex Hull algorithms. You might be able to modify one of the algorithms to get your extreme points and go from there.

iCanHasFay
  • 662
  • 5
  • 12
0

Ok, it seems I made working solution:

http://mrpyo.github.com/Polygon/

It's ActionScript so you should have no problem translating it into JavaScript. I can explain used algorithm if somebody is interested...

zduny
  • 2,481
  • 1
  • 27
  • 49