Is there a one-line function that generates a triangle wave?

Question

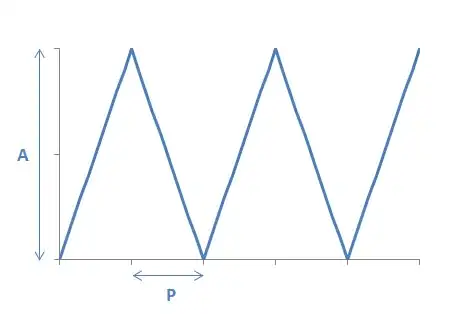
In a similar way that modulo generates a sawtooth wave. It doesn't have to be continuous.

here is what i mean:

int m = 10;
int x = 0;
int i = 0;
while (i < m*3) {
    printf("%d ", x);
    x++;
    x = x % m;
    i++;
}

generates a sequence 0..9, three times which looks like this:

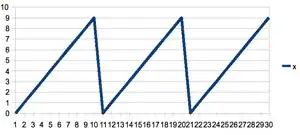
note that the slope on the right side of the peak is just a graphing artifact

The one-liner in this case is x = i++ % m

---

What I want is this:

If you know one-liners for the other wave forms (sine, square), that would be good to know as well.

Update: everyone's answers have been very helpful and I have a follow-up question.

What would be added to the triangle wave function to make the slope of the lines curve in or out like this:

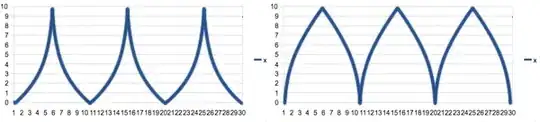
Thanks everyone, your varied answers helped me see the problem from a larger perspective. Special thanks to Noldorin for his take on extending the equation to quadratic curves.

Answer 1

Triangular Wave

y = abs((x++ % 6) - 3);

This gives a triangular wave of period 6, oscillating between 3 and 0.

Square Wave

y = (x++ % 6) < 3 ? 3 : 0;

This gives a regular square wave of period 6, oscillating between 3 and 0.

Sine Wave

y = 3 * sin((float)x / 10);

This gives a sine wave of period 20 pi, oscillating between 3 and -3.

---

Update:

Curvy Triangular Wave

To get a variation of the triangular wave that has curves rather than straight lines, you just need to introduce an exponent into the equation to make it quadratic.

Concave curves (i.e. x^2 shape):

y = pow(abs((x++ % 6) - 3), 2.0);

Concave curves (i.e. sqrt(x) shape):

y = pow(abs((x++ % 6) - 3), 0.5);

Alternatively to using the pow function, you could simply define a square function and use the sqrt function in math.h, which would probably improve performance a bit.

Also, if you want to make the curves steeper/shallower, just try changing the indices.

---

In all of these cases you should easily be able to adjust constants and add scaling factors in the right places to give variations of the given waveforms (different periods, ampltiudes, asymmetries, etc.).

Answer 2

Expanding on Eric Bainville's answer:

y = (A/P) * (P - abs(x % (2*P) - P) )

Where x is a running integer, and y the triangle wave output. A is the amplitude of the wave, and P the half-period. For instance, A=5 will produce a wave which goes from 0 to 5; P=10 will produce a wave with a period of 20. The wave starts at y=0 for x=0.

Note that y will be a floating-point number unless P is a factor of A. And, yes, for the mathematical purists: A is technically twice the amplitude of the wave, but look at the picture below and you'll understand what I mean.

Visualised:

Answer 3

x = m - abs(i % (2*m) - m)

Answer 4

I know this is an old post but for anyone that is searching for something similar I recommend looking at. http://en.wikipedia.org/wiki/Triangle_wave

The last formula y(x)=(2a/π)arcsin(sin((2π/p)*x))

or.

(2 * amplitudeConstant / Math.PI) * Math.Asin(Math.Sin(2 * (Math.PI / periodConstant) * Convert.ToDouble(variableX)))

Answer 5

y = abs( amplitude - x % (2*amplitude) )

Changing the wavelength just needs a factor for x.

Edit: What I call amplitude is actually not the amplitude, but the maximum value (i.e. 5 if the curve oscillates betwen 0 and 5). The amplitude in the mathematical sense is half of that. But you get the point.

Answer 6

Try this:

x = m - abs(m - 2*(i++ % m))

Answer 7

Here is a periodic function that looks like a distant sine approximation; essentially it's a Sinuating paraboloid, using X squared:

function  xs ( xx : float ): float{

    var xd =Mathf.Abs((Mathf.Abs(xx) % 2.4) - 1.2);

    if (  Mathf.Abs(Mathf.Abs(xx) % 4.8)  > 2.4){ 
        xd=(-xd*xd)+2.88;
    }else{
        xd = xd*xd;
    }

    return xd;

}

Answer 8

I've tested it with a simple loop and you guys haven't answered the man's question at all. Cut and pasting won't help people. No wonder so many mass media hoaxes have so much success. With a folks that repeats mistakes of others that cannot be any surprise is it. And people even give positive reputation rates for these wrong answers?! Unbelievable! But again, this parallels with my previous remark.

So first off we are going to explain to our folks what a TRIANGLE wave IS. Well it is a wave which has a period consisting of TWO equal sloped ramps. A ramp sloped UP and a ramp equally as the first but sloped DOWN contrary to a SAWTOOTH which has a ramp sloped UP or a ramp sloped DOWN repeated after a reversed talud.

PS: The last one who gave "y(x)=(2a/π)arcsin(sin((2π/p)*x))" is too complicated, we are looking for a fast c++ routine so trigonometry is absolutely out of the question.

Test routine:

(...)

for (byte V=0; V<255; V++)
{
unsigned int x = evenramp(V);
plotRGB(0,0,x,x,x);
delay(100); // make sure you have your own delay function declared of course

/* use your own graphic function !!! plotRGB(row,column,R,G,B) */
/* the light intensity will give you the change of value V in time */
/* all functions suggested as answer give SAWTOOTH and NOT TRIANGLE */
/* it is a TRIANGLE the man wants */
}

float triangleattempt(unsigned int x) // place any answered formula after '255 *' behind return.
{
return 255 * (255 - abs(255 - 2*(x % 255))); // this will show a SAWTOOTH
}

//All given answers up to now excluding "function  xs ( xx : float ): float" (this is not the requested one-liner, sorry) that are not a symmetrical triangle wave

// m - abs(i % (2*m) - m); (this is still a SAWTOOTH wave and not a TRIANGLE wave)
// abs((x++ % 6) - 3); (this is still a SAWTOOTH wave and not a TRIANGLE wave)
// abs(amplitude - x % (2*amplitude)); (this is still a SAWTOOTH wave and not a TRIANGLE wave)

=> I found a source which tells exactly what the answer is in mathematical notation: http://mathworld.wolfram.com/TriangleWave.html

I have tested the formula on a Linux program called KmPlot. Linux users can get kmplot via the root terminal typing apt-get install kmplot and if that doesn't work try using the regular terminal and type sudo apt-get install kmplot and if that doesn't work watch this youtube video for general instructions on installing a Linux program http://www.youtube.com/watch?v=IkhcwxC0oUg

SO A CORRECT ANSWER to the thread question is an example of a symmetrical triangle function declaration in c++ form shown below:

(...)

int symetrictriangle(float x)
{
unsigned int period = 30; // number of increases of x before a new cycle begins
unsigned int amplitude = 100; // top to bottom value while the bottom value is always zero
return amplitude * 2 * abs(round(x/period)-(x/period));
}

(...)

Cheerz!