You need something more elementary here, there isn't much reason to go for fancy methods. Your figures are already binary ones, and their shapes are very similar overall.
One initial idea: consider the upper points and bottom points in a certain image and form a upper hull and a bottom hull (simply a hull, not a convex hull or anything else). A point is said to be an upper point (respec. bottom point) if, given a column i, it is the first point starting at the top (bottom) of the image that is not a background point in i. Also, your image is mostly one single connected component (in some cases there are vertical bars separated, but that is fine), so you can discard small components easily. This step is important for your situation because I saw there are some figures with some form of noise that is irrelevant to the rest of the image. Considering that a connected component with less than 100 points is small, these are the hulls you get for the respective images included in the question:


The blue line is indicating the upper hull, the green line the bottom hull. If it is not apparent, when we consider the regional maxima and regional minima of these hulls we obtain the same amount in both of them. Furthermore, they are all very close except for some displacement in the y axis. If we consider the mean x position of the extrema and plot the lines of both images together we get the following figure. In this case, the lines in blue and green are for the second image, and the lines in red and cyan for the first. Red dots are in the mean x coordinate of some regional minima, and blue dots the same but for regional maxima (these are our points of interest). (The following image has been resized for better visualization)
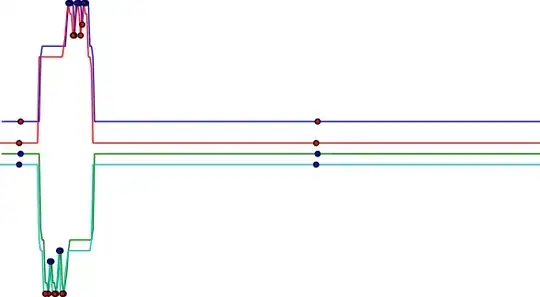
As you can see, you get many nearly overlapping points without doing anything. If we do even less, i.e. not even care about this overlapping, and proceed to classify your images in the trivial way: if an image a and another image b have the same amount of regional maxima in the upper hull, the same amount of regional minima in the upper hull, the same amount of regional maxima in the bottom hull, and the same amount of regional minima in the bottom hull, then a and b belong to the same class. Doing this for all your images, all images are correctly grouped except for the following situation:

In this case we have only 3 maxima and 3 minima for the upper hull in the first image, while there are 4 maxima and 4 minima for the second. Following you see the plots for the hulls and points of interest obtained:

As you can notice, in the second upper hull there are two extrema very close. Smoothing this curve eliminates both extrema, making the images match by the trivial method. Also, note that if you draw a rectangle around your images, then this method will tell they are all equal. In that case you will want to compare multiple hulls, discarding the points in the current hull and constructing other ones. Nevertheless, this method is able to group all your images correctly given they are all very simple and mostly noisy-free.