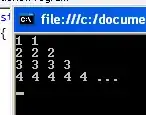
In my answer I will ignore the last result you had: Adam, Bob: 1, 2, 3, because it is an exception logically. Skip to the end to see my output.
Explanation:
The idea would be iterating combinations of "which group an element will belong to".
Say you have elements "a, b, c", and you have groups "1, 2", lets have an array of size 3, as the number of elements, which will contain all possible combinations of the groups "1, 2", WITH repetition:
{1, 1, 1} {1, 1, 2} {1, 2, 1} {1, 2, 2}
{2, 1, 1} {2, 1, 2} {2, 2, 1} {2, 2, 2}
Now we shall take each group, and sort of make a key-value collection out of it, with the following logic:
Group of elements[i] will be the value of comb[i].
Example with {1, 2, 1}:
a: group 1
b: group 2
c: group 1
And in a different view, the way you wanted it:
group 1: a, c
group 2: b
After all that, you just have to filter all the combinations that do not contain all groups, because you wanted all groups to have at least one value.
So you should check if all groups appear in a certain combination and filter the ones that don't match, so you'll be left with:
{1, 1, 2} {1, 2, 1} {1, 2, 2}
{2, 1, 2} {2, 2, 1} {2, 1, 1}
Which will result in:
1: a, b
2: c
1: a, c
2: b
1: a
2: b, c
1: b
2: a, c
1: c
2: a, b
1: b, c
2: a
This group-breaking combination logic will work for bigger amount of elements and groups as well. Here is my implementation, which can probably be done better, because even I got a little lost in there while I coded it (it's really not an intuitive problem hehe), but it works good.
Implementation:
public static IEnumerable<ILookup<TValue, TKey>> Group<TKey, TValue>
(List<TValue> keys,
List<TKey> values,
bool allowEmptyGroups = false)
{
var indices = new int[values.Count];
var maxIndex = values.Count - 1;
var nextIndex = maxIndex;
indices[maxIndex] = -1;
while (nextIndex >= 0)
{
indices[nextIndex]++;
if (indices[nextIndex] == keys.Count)
{
indices[nextIndex] = 0;
nextIndex--;
continue;
}
nextIndex = maxIndex;
if (!allowEmptyGroups && indices.Distinct().Count() != keys.Count)
{
continue;
}
yield return indices.Select((keyIndex, valueIndex) =>
new
{
Key = keys[keyIndex],
Value = values[valueIndex]
})
.OrderBy(x => x.Key)
.ToLookup(x => x.Key, x => x.Value);
}
}
Usage:
var employees = new List<string>() { "Adam", "Bob"};
var jobs = new List<string>() { "1", "2", "3"};
var c = 0;
foreach (var group in CombinationsEx.Group(employees, jobs))
{
foreach (var sub in group)
{
Console.WriteLine(sub.Key + ": " + string.Join(", ", sub));
}
c++;
Console.WriteLine();
}
Console.WriteLine(c + " combinations.");
Output:
Adam: 1, 2
Bob: 3
Adam: 1, 3
Bob: 2
Adam: 1
Bob: 2, 3
Adam: 2, 3
Bob: 1
Adam: 2
Bob: 1, 3
Adam: 3
Bob: 1, 2
6 combinations.
UPDATE
Combined keys combinations prototype:
public static IEnumerable<ILookup<TKey[], TValue>> GroupCombined<TKey, TValue>
(List<TKey> keys,
List<TValue> values)
{
// foreach (int i in Enumerable.Range(1, keys.Count))
for (var i = 1; i <= keys.Count; i++)
{
foreach (var lookup in Group(Enumerable.Range(0, i).ToList(), keys))
{
foreach (var lookup1 in
Group(lookup.Select(keysComb => keysComb.ToArray()).ToList(),
values))
{
yield return lookup1;
}
}
}
/*
Same functionality:
return from i in Enumerable.Range(1, keys.Count)
from lookup in Group(Enumerable.Range(0, i).ToList(), keys)
from lookup1 in Group(lookup.Select(keysComb =>
keysComb.ToArray()).ToList(),
values)
select lookup1;
*/
}
There's still a little problem of duplicates, but it produces all results.
Here is what I would use to remove duplicates, as a temporary solution:
var c = 0;
var d = 0;
var employees = new List<string> { "Adam", "Bob", "James" };
var jobs = new List<string> {"1", "2"};
var prevStrs = new List<string>();
foreach (var group in CombinationsEx.GroupCombined(employees, jobs))
{
var currStr = string.Join(Environment.NewLine,
group.Select(sub =>
string.Format("{0}: {1}",
string.Join(", ", sub.Key),
string.Join(", ", sub))));
if (prevStrs.Contains(currStr))
{
d++;
continue;
}
prevStrs.Add(currStr);
Console.WriteLine(currStr);
Console.WriteLine();
c++;
}
Console.WriteLine(c + " combinations.");
Console.WriteLine(d + " duplicates.");
Output:
Adam, Bob, James: 1, 2
Adam, Bob: 1
James: 2
James: 1
Adam, Bob: 2
Adam, James: 1
Bob: 2
Bob: 1
Adam, James: 2
Adam: 1
Bob, James: 2
Bob, James: 1
Adam: 2
7 combinations.
6 duplicates.
Note that it will also produce non-combined groups (if possible - because no empty groups are allowed). To produce ONLY combined-keys you will need to replace this:
for (var i = 1; i <= keys.Count; i++)
With this:
for (var i = 1; i < keys.Count; i++)
In the beginning of the GroupCombined method. Test the method with three employees and three jobs to see how it works exactly.
ANOTHER EDIT:
A better duplicates-handling would be handling duplicate key-combinations in the GroupCombined level:
public static IEnumerable<ILookup<TKey[], TValue>> GroupCombined<TKey, TValue>
(List<TKey> keys,
List<TValue> values)
{
for (var i = 1; i <= keys.Count; i++)
{
var prevs = new List<TKey[][]>();
foreach (var lookup in Group(Enumerable.Range(0, i).ToList(), keys))
{
var found = false;
var curr = lookup.Select(sub => sub.OrderBy(k => k).ToArray())
.OrderBy(arr => arr.FirstOrDefault()).ToArray();
foreach (var prev in prevs.Where(prev => prev.Length == curr.Length))
{
var isDuplicate = true;
for (var x = 0; x < prev.Length; x++)
{
var currSub = curr[x];
var prevSub = prev[x];
if (currSub.Length != prevSub.Length ||
!currSub.SequenceEqual(prevSub))
{
isDuplicate = false;
break;
}
}
if (isDuplicate)
{
found = true;
break;
}
}
if (found)
{
continue;
}
prevs.Add(curr);
foreach (var group in
Group(lookup.Select(keysComb => keysComb.ToArray()).ToList(),
values))
{
yield return group;
}
}
}
}
As it seems, it would be smart to add constraints to the method so that TKey will be ICompareable<TKey> and maybe also IEquatable<TKey>.
This results with 0 duplicates in the end.