I am starting to learn CUDA and I think calculating long digits of pi would be a nice, introductory project.
I have already implemented the simple Monte Carlo method which is easily parallelize-able. I simply have each thread randomly generate points on the unit square, figure out how many lie within the unit circle, and tally up the results using a reduction operation.
But that is certainly not the fastest algorithm for calculating the constant. Before, when I did this exercise on a single threaded CPU, I used Machin-like formulae to do the calculation for far faster convergence. For those interested, this involves expressing pi as the sum of arctangents and using Taylor series to evaluate the expression.
An example of such a formula:
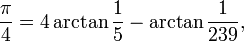
Unfortunately, I found that parallelizing this technique to thousands of GPU threads is not easy. The problem is that the majority of the operations are simply doing high precision math as opposed to doing floating point operations on long vectors of data.
So I'm wondering, what is the most efficient way to calculate arbitrarily long digits of pi on a GPU?