I have read about some of the methods for calculating Fibonacci with efficient time complexity following are some of them -
Method 1 - Dynamic Programming
Now here the substructure is commonly known hence I'll straightly Jump to the solution -
static int fib(int n)
{
int f[] = new int[n+2]; // 1 extra to handle case, n = 0
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
A space-optimized version of above can be done as follows -
static int fib(int n)
{
int a = 0, b = 1, c;
if (n == 0)
return a;
for (int i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
Method 2- ( Using power of the matrix {{1,1},{1,0}} )
This an O(n) which relies on the fact that if we n times multiply the matrix M = {{1,1},{1,0}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at row and column (0, 0) in the resultant matrix. This solution would have O(n) time.
The matrix representation gives the following closed expression for the Fibonacci numbers:
fibonaccimatrix
static int fib(int n)
{
int F[][] = new int[][]{{1,1},{1,0}};
if (n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
/*multiplies 2 matrices F and M of size 2*2, and
puts the multiplication result back to F[][] */
static void multiply(int F[][], int M[][])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
/*function that calculates F[][] raise to the power n and puts the
result in F[][]*/
static void power(int F[][], int n)
{
int i;
int M[][] = new int[][]{{1,1},{1,0}};
// n - 1 times multiply the matrix to {{1,0},{0,1}}
for (i = 2; i <= n; i++)
multiply(F, M);
}
This can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the previous method.
static int fib(int n)
{
int F[][] = new int[][]{{1,1},{1,0}};
if (n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
static void multiply(int F[][], int M[][])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
static void power(int F[][], int n)
{
if( n == 0 || n == 1)
return;
int M[][] = new int[][]{{1,1},{1,0}};
power(F, n/2);
multiply(F, F);
if (n%2 != 0)
multiply(F, M);
}
Method 3 (O(log n) Time)
Below is one more interesting recurrence formula that can be used to find nth Fibonacci Number in O(log n) time.
If n is even then k = n/2:
F(n) = [2*F(k-1) + F(k)]*F(k)
If n is odd then k = (n + 1)/2
F(n) = F(k)*F(k) + F(k-1)*F(k-1)
How does this formula work?
The formula can be derived from the above matrix equation.
fibonaccimatrix
Taking determinant on both sides, we get
(-1)n = Fn+1Fn-1 – Fn2
Moreover, since AnAm = An+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product)
FmFn + Fm-1Fn-1 = Fm+n-1
By putting n = n+1,
FmFn+1 + Fm-1Fn = Fm+n
Putting m = n
F2n-1 = Fn2 + Fn-12
F2n = (Fn-1 + Fn+1)Fn = (2Fn-1 + Fn)Fn (Source: Wiki)
To get the formula to be proved, we simply need to do the following
If n is even, we can put k = n/2
If n is odd, we can put k = (n+1)/2
public static int fib(int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return (f[n] = 1);
// If fib(n) is already computed
if (f[n] != 0)
return f[n];
int k = (n & 1) == 1? (n + 1) / 2
: n / 2;
// Applyting above formula [See value
// n&1 is 1 if n is odd, else 0.
f[n] = (n & 1) == 1? (fib(k) * fib(k) +
fib(k - 1) * fib(k - 1))
: (2 * fib(k - 1) + fib(k))
* fib(k);
return f[n];
}
Method 4 - Using a formula
In this method, we directly implement the formula for the nth term in the Fibonacci series. Time O(1) Space O(1)
Fn = {[(√5 + 1)/2] ^ n} / √5
static int fib(int n) {
double phi = (1 + Math.sqrt(5)) / 2;
return (int) Math.round(Math.pow(phi, n)
/ Math.sqrt(5));
}
Reference: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibFormula.html
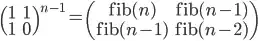 . It shows nice linear resulting behavior because in
. It shows nice linear resulting behavior because in 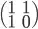 and
and 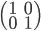 .
.