Motion planning without a graph across an infinite plane

Question

An object is positioned at A and wants to move to B. I want to calculate a movement vector there that doesn't move within the distance D of the to-be-avoided points in array C.

So if the move vector (B-A) normalized and multiplied with the objects speed would bring it within D of any point in C the vector is rotated so that it doesn't.

This is in two dimensions. Also, if this operation has a name, please make a comment or edit this question yourself as I had no idea of what to call it.

Also, my first instinct was to divide the active area into nodes and run a A* but I want to try the mathematical approach on this one, a few experiments with flocking gives me the impression that it can be done.

Update (from comments): This image is very close to the solution I want:

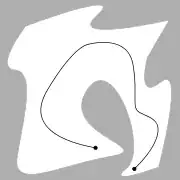
Assuming we start at the point to the left, we start turning right towards the goal (the other point), we detect a wall on the right so we stop turning and move forward. The wall is gone so we are allowed to start turning towards the goal again, and so on. I know this may cause the object to not get there at all, but I want to define a behavior, not necessarily a solution, if you know what I mean.

Update2: Translating the active area into a set of nodes might prove inefficient. A* and other heuristic graph traversal algorithms are great for low dimensional problems. But the area I want to move across is infinite in size and only has a handful of obstacles scattered across it. The nodes themselves, or rather the potential positions, are infinitely small. This could of course be optimized with a quad tree of some sort but I have a feeling simple movement vectors that are in some way rotated and interpolated can solve this as well.

Answer 1

I hear this called motion planning, and pathfinding (as mentioned above)

There are a lot of algorithms, but from your description, a visibility graph might be a good start. You have a graph with points A, B, and polygons around each point in C (you could also do it with circles by calculating tangent lines from each point, I believe). You calculate edges as potential paths between the points. Here's a slide show which explains it better.

Then, on top of the visibilty graph, apply a search algorithm like A* (a heuristic search) to find the most optimal path through the graph.

However, you should consider what you are looking for. The above approach will find a shortest path by sticking extremely close to all corners, but other algorithms might better fit your idea of optimality.

Answer 2

Also on the page you linked to in your answer is a pretty good discussion of steering behaviours in general.

In particular, look at his pages for containment and path following for good examples.

Steering Behaviors for Autonomous Characters

Answer 3

You could consider using potential fields. This offers a way to avoid "hugging the edges" of the obstacles.

But note that, like the A* algorithm, this requires that you quantize the state space, and may therefore be quite computationally intensive depending on how much accuracy you need.

Answer 4

I found a quite verbose description of a flocking routine on this page.

Use the separation rule for all obstacles, and alignment only towards the goal position (since we have no flock mates) and (for the same reason) ignoring the cohesion rule.

I wounder if that would yield the desired effect.