How do Suffix Trees work?

Question

I'm going through the data structures chapter in The Algorithm Design Manual and came across Suffix Trees.

The example states:

Input:

XYZXYZ$
 YZXYZ$
  ZXYZ$
   XYZ$
    YZ$
     Z$
      $

Output:

I'm not able to understand how that tree gets generated from the given input string. Suffix trees are used to find a given Substring in a given String, but how does the given tree help towards that? I do understand another given example of a trie shown below, but if the below trie gets compacted to a suffix tree, then what would it look like?

Answer 1

The standard efficient algorithms for constructing a suffix tree are definitely nontrivial. The main algorithm for doing so is called Ukkonen's algorithm and is a modification of the naive algorithm with two extra optmizations. You are probably best off reading this earlier question for details on how to build it.

You can construct suffix trees by using the standard insertion algorithms on radix tries to insert each suffix into the tree, but doing so wlil take time O(n²), which can be expensive for large strings.

As for doing fast substring searching, remember that a suffix tree is a compressed trie of all the suffixes of the original string (plus some special end-of-string marker). If a string S is a substring of the initial string T and you had a trie of all the suffixes of T, then you could just do a search to see if T is a prefix of any of the strings in that trie. If so, then T must be a substring of S, since all its characters exist in sequence somewhere in T. The suffix tree substring search algorithm is precisely this search applied to the compressed trie, where you follow the appropriate edges at each step.

Hope this helps!

Answer 2

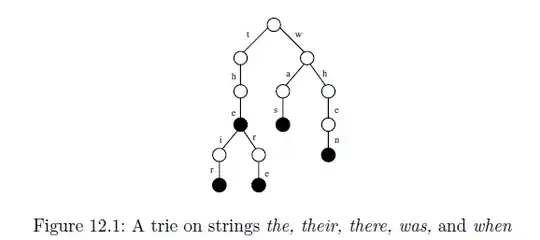
I'm not able to understand how that tree gets generated from the given input string.

You essentially create a patricia trie with all the suffixes you've listed. When inserting into a patricia trie, you search the root for a child starting with the first char from the input string, if it exists you continue down the tree but if it doesn't then you create a new node off the root. The root will have as many children as unique characters in the input string ($, a, e, h, i, n, r, s, t, w). You can continue that process for each character in the input string.

Suffix trees are used to find a given Substring in a given String, but how does the given tree help towards that?

If you are looking for substring "hen" then start searching from the root for a child which starts with "h". If the length of the string of in child "h" then continue to process child "h" until you've come to the end of the string or you get a mismatch of characters in input string and child "h" string. If you match all of child "h", i.e. input "hen" matches "he" in child "h" then move on to the children of "h" until you get to "n", if it fail to find a child beginning with "n" then the substring doesn't exist.

Compact Suffix Trie code:

└── (black)
    ├── (white) as
    ├── (white) e
    │   ├── (white) eir
    │   ├── (white) en
    │   └── (white) ere
    ├── (white) he
    │   ├── (white) heir
    │   ├── (white) hen
    │   └── (white) here
    ├── (white) ir
    ├── (white) n
    ├── (white) r
    │   └── (white) re
    ├── (white) s
    ├── (white) the
    │   ├── (white) their
    │   └── (white) there
    └── (black) w
        ├── (white) was
        └── (white) when

Suffix Tree code:

String = the$their$there$was$when$
End of word character = $
└── (0)
    ├── (22) $
    ├── (25) as$
    ├── (9) e
    │   ├── (10) ir$
    │   ├── (32) n$
    │   └── (17) re$
    ├── (7) he
    │   ├── (2) $
    │   ├── (8) ir$
    │   ├── (31) n$
    │   └── (16) re$
    ├── (11) ir$
    ├── (33) n$
    ├── (18) r
    │   ├── (12) $
    │   └── (19) e$
    ├── (26) s$
    ├── (5) the
    │   ├── (1) $
    │   ├── (6) ir$
    │   └── (15) re$
    └── (29) w
        ├── (24) as$
        └── (30) hen$

Answer 3

A suffix tree basically just compacts runs of letters together when there are no choices to be made. For example, if you look at the right side of the trie in your question, after you've seen a w, there are really only two choices: was and when. In the trie, the as in was and the hen in when each still have one node for each letter. In a suffix tree, you'd put those together into two nodes holding as and hen, so the right side of your trie would turn into: