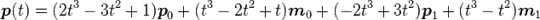Cubic/Curve Smooth Interpolation in C#

Question

Below is a cubic interpolation function:

public float Smooth(float start, float end, float amount)
{
    // Clamp to 0-1;
    amount = (amount > 1f) ? 1f : amount;
    amount = (amount < 0f) ? 0f : amount;

    // Cubicly adjust the amount value.
    amount = (amount * amount) * (3f - (2f * amount));

    return (start + ((end - start) * amount));
}

This function will cubically interpolate between the start and end value given an amount between 0.0f - 1.0f. If you were to plot this curve, you'd end up with something like this:

Expired Imageshack image removed

The cubic function here is:

    amount = (amount * amount) * (3f - (2f * amount));

How do I adjust this to produce two produce tangents in and out?

To produce curves like this: (Linear start to cubic end)

Expired Imageshack image removed

As one function

and like this as another: (Cubic start to linear end)

Expired Imageshack image removed

Anyone got any ideas? Thanks in advance.

Voted to close this question since it relies on images to show what the question/problem is, and those images are apparently long gone. The question as it stands thus (in my opinion) has no value, nor has the answer, because nobody knows what question those answers answer. — Lasse V. Karlsen, Aug 15 '15 at 19:50

score 12 · Accepted Answer · edited Feb 08 '17 at 14:13

12

What you want is a Cubic Hermite Spline:

alt text

where p0 is the start point, p1 is the end point, m0 is the start tangent, and m1 is the end tangent

edited Feb 08 '17 at 14:13

Community

1
1

answered Jul 18 '09 at 01:18

Donnie DeBoer

2,517
15
14

1

thanks Robert, for making it look WAY prettier :) – Donnie DeBoer Jul 18 '09 at 01:31
1

Yes. This is the way to do this. A piecewise cubic Hermite interpolant has the nice property that it is simply assured to be both continuous and differentiable across the break points, because the value and first derivative at each end of an interval is given. This is, IMHO, a very pretty way to build up a piecewise cubic. – Jul 18 '09 at 08:25

Donnie DeBoer · Answer 2 · 2009-07-18T00:45:43.983

3

you could have a linear interpolation and a cubic interpolation and interpolate between the two interpolation functions.

ie.

cubic(t) = cubic interpolation
linear(t) = linear interpolation
cubic_to_linear(t) = linear(t)*t + cubic(t)*(1-t)
linear_to_cubic(t) = cubic(t)*t + linear(t)*(1-t)

where t ranges from 0...1

edited Jul 18 '09 at 00:45

answered Jul 18 '09 at 00:36

Donnie DeBoer

2,517
15
14

I'll see if I can get your solution working. However, ideally I'd rather just adjust the cubic function in the method: amount = (amount * amount) * (3f - (2f * amount)); I'm assuming this can be done fairly easily, I'm just not sure how. – Rob Jul 18 '09 at 00:53
1

If you want to have tangents, use the Cubic Hermite Spline I posted below – Donnie DeBoer Jul 18 '09 at 01:33

score 0 · Answer 3 · answered Dec 22 '13 at 02:18

Well, a simple way would be this:

-Expand your function by 2 x and y
-Move 1 to the left and 1 down
Example: f(x) = -2x³+3x²
g(x) = 2 * [-2((x-1)/2)³+3((x-1)/2)²] - 1

Or programmatically (cubical adjusting):

double amountsub1div2 = (amount + 1) / 2;
amount = -4 * amountsub1div2 * amountsub1div2 * amountsub1div2 + 6 * amountsub1div2 * amountsub1div2 - 1;

For the other one, simply leave out the "moving":

g(x) = 2 * [-2(x/2)³+3(x/2)²]

Or programmatically (cubical adjusting):

double amountdiv2 = amount / 2;
amount = -4 * amountdiv2 * amountdiv2 * amountdiv2 + 6 * amountdiv2 * amountdiv2;

Cubic/Curve Smooth Interpolation in C#

3 Answers3

Linked