I have a three-dimensional fenwick tree data structure.
I need to calculate sum on some segment from (x0, y0, z0) to (x, y, z)
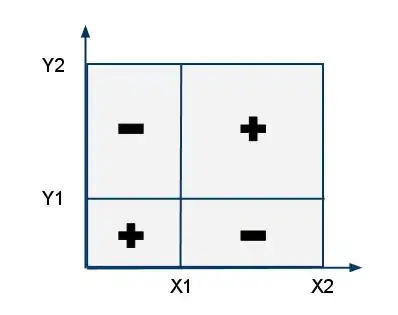
What is the formula for inclusion-exclusion? For instance, for 2D variant it is
s = sum(x, y) - sum(x, y0 - 1) - sum(x0 - 1, y) + sum(x0 - 1, y0 - 1)
Thanks in advance
http://www.comp.nus.edu.sg/~stevenha/ft.pdf
Here is 2D case: