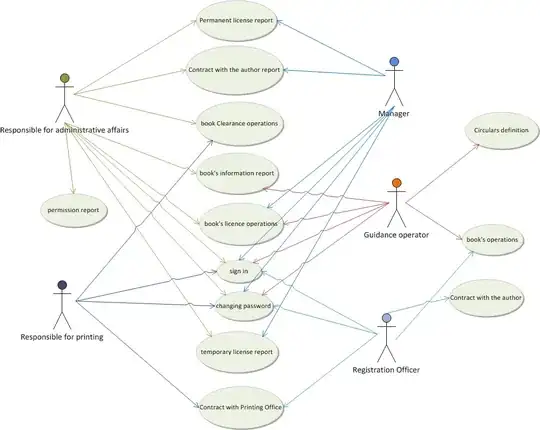
all, I'm trying to understand how exactly we are to calculate the number of inversions between two arrays.
Let's say, for example, we have the following two arrays:
A = [1, 2, 3, 4, 5, 6] B = [6, 3, 5, 4, 2, 1]
How would I calculate the number of inversions conceptually? That is, just looking at these two arrays, disregarding the coding involved.
Also, I know the convention of drawing line segments between the two arrays, but I'm trying to gain a deeper understanding here.
Thank you!