Given a number, find whether it is brilliant or not

Question

It's a programming puzzle which goes like: "A number is said to be brilliant if the product of all digits of its substrings have a unique value."

Example : 263 (2, 6, 3, 2*6 = 12, 6*3 = 18) is brilliant.

But 236 (2, 3, 6, 2*3 = 6, 3*6 = 18) is not brilliant.

We take only substrings, not subsequences.

I was thinking maybe we can apply Dynamic Programming here because of repeated product calculations? What other solutions can we have for it? (This isn't a homework question.)

Answer 1

Here's one way of solving it using dynamic programming:

Assume we have the number d₀ d₁ ... d_N as input.

The idea is to create a table, where cell (i, j) store the product d_i · d_i+1 · ... · d_j. This can be done efficiently since the cell at (i, j) can be computed by multiplying the number at (i-1, j) by d_i.

Since i (the start index) must be less than or equal to j (the end index), we'll focus on the lower left triangle of the table.

After generating the table, we check for duplicate entries.

Here's a concrete example solution for input 2673:

1. We allocate a matrix, M, with dimensions 4 × 4.

   

2. We start by filling in the diagonals, M_i,i with d_i:

   

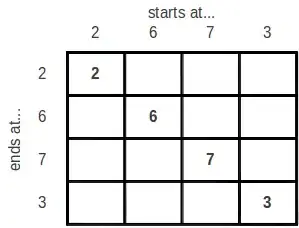
3. We then go row by row, and fill in M_i,j with d_i ·M_i-1,j

   

4. The result looks like

   

5. To check for duplicates, we collect the products (2, 12, 6, 84, 42, 7, 252, 126, 21, 3), sort them (2, 3, 6, 7, 12, 21, 42, 84, 126, 252), and loop through to see if two consecutive numbers are equal. If so we return false, otherwise true.

In Java code:

Here's a working DP solution, O(n²).

public static boolean isColorful(int num) {

    // Some initialization
    String str = "" + num;
    int[] digits = new int[str.length()];
    for (int i = 0; i < str.length(); i++)
        digits[i] = str.charAt(i) - '0';
    int[][] dpmatrix = new int[str.length()][str.length()];

    // Fill in diagonal: O(N)
    for (int i = 0; i < digits.length; i++)
        dpmatrix[i][i] = digits[i];

    // Fill in lower left triangle: O(N^2)
    for (int i = 0; i < str.length(); i++)
        for (int j = 0; j < i; j++)
            dpmatrix[i][j] = digits[i] * dpmatrix[i-1][j];

    // Check for dups: O(N^2)
    int[] nums = new int[digits.length * (digits.length+1) / 2];
    for (int i = 0, j = 0; i < digits.length; i++, j += i)
        System.arraycopy(dpmatrix[i], 0, nums, j, i+1);

    Arrays.sort(nums);

    for (int i = 0; i < nums.length - 1; i++)
        if (nums[i] == nums[i+1])
            return false;

    return true;
}

For DP-interested readers I can recommend the somewhat similar question/answer over here:

• Find the number of occurrences of a subsequence in a string

Answer 2

Using dynamic programming is probably the way to go: Instead of calculating all O(n^2) substrings, and then using ~n multiplication commands to calculate each of them, store the results of previous caclulation in a matrix M, where M(i,j) is the result of the substring of length j, starting from position i.

(i.e, if your number is 123456789, then M(1,5) is 5!, and M(1,6) is 6!, which only requires multiplying M(1,5) by 6 - constant work)

This will improve the running time from O(n^3) for n digits to O(n^2).

Answer 3

A dynamic programming solution is really not necessary, as there are no brilliant numbers with a large number of digits (if any digit appears more than once, the number is not brilliant).

Here is a list of every brilliant number. There are 57,281 total.

This file took less than a second to generate on my PC, even without using dynamic programming :)

Answer 4

if we don't consider the number as a large string then hashing can help;

 int brill(int A) {
    map<long long int,bool> m;
    vector<int> arr(10,0);
    int i=0;
    while(A){
        arr[i++]=A%10;
        A/=10;
    }

    for(int j=0;j<i;j++){

        long long int temp=1;

        for(int k=j;k>=0;k--){
            temp*=arr[k];

            if(m.find(temp)!=m.end()){
                return 0;
            }
            else{
                m[temp]=true;
            }
        }
    }
    return 1;

}

Answer 5

n is the string containing the number.

Since the number can't be greater than 8 digits before a failure state its O(1).

function isBrill(n) {
  var set = {};
  set[parseInt(n.charAt(0))] = true;
  for(var i=0; i < n.length - 1; i++) {
    var a = parseInt(n.charAt(i));
    var b = parseInt(n.charAt(i+1));
    if(set[b] === true) { return false; }
    set[b] = true;
    if(set[a * b] === true) { return false; }
    set[a * b] = true;
  }
  return true;
}
isBrill("263"); // true
isBrill("236"); // false