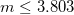I am trying to encode a message using a public key provided to me by an external site using Python M2Crypto's RSA. Essentially, I am doing something like this:
from M2Crypto import RSA
import os
rsa = RSA.load_pub_key(os.path.join(BASE_PATH, 'external_site.pem'))
rsa_result = rsa.public_encrypt(message, 3).encode('base64')
If I don't use padding when encrypting I receive the error:
RSAError: data too small for key size
I understand why there's an upper limit on the message length (the modulus for the RSA encryption), but I don't understand why there would be a lower limit. Could someone explain this or point me in the right direction to figure it out?



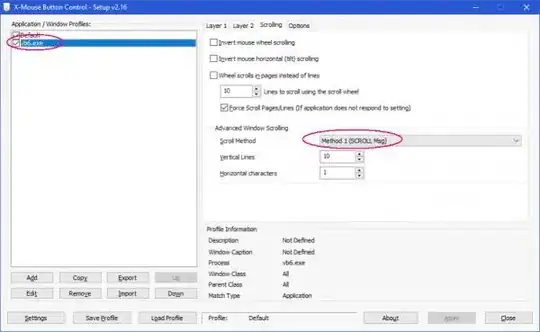

![\sqrt[e]{n} > m > (n - 1)](../../images/3830254711.webp)