4

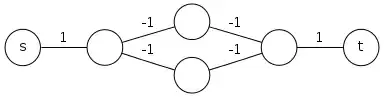
My problem is the following:

I have an undirected graph. Each edge has a cost (or weight). One of the nodes is labelled S. I want to start from S and visit every node at least once. Visiting a node multiple times is allowed. Travelling along an edge multiple times is allowed, although that would make the solution more expensive -- travelling an edge with cost of 3 twice will add 6 to the cost of the total path. The graph has some "dead-end" nodes, so sometimes we have to travel an edge more than once.

What is a fast algorithm to do this? Is this a well known problem?

What I'm looking for:

Reasonably fast -- The relative size of the graph we are talking about here is order of 40 - 50 nodes. So the algorithm hopefully won't take longer than 10 - 15 seconds.

Reasonably optimal -- I'm not looking for absolute optimality. Any interesting heuristic to guide the search so that the solution will be near optimal is good enough.

I will be writing this in python. So if you know of any python implementation of the algorithm, that's best.

Thanks for any help.

darksky
  • 1,955
  • 16
  • 28
  • Your problem is similar to [TSP](http://en.wikipedia.org/wiki/Travelling_salesman_problem) and for this problem or variations there are already a number of heuristics in the literature. – CRM Sep 05 '12 at 16:31
  • @bacchus, I would posit that the TSP adds a HUGE constraint that is not stated above. – im so confused Sep 05 '12 at 16:33
  • bah bacchus beat me to it ... this is one of those NP probs :P @AkshayaAnnavajhala you mean ending at same node as start(thats not ALWAYS a condition of TSP i dont think)? – Joran Beasley Sep 05 '12 at 16:33
  • @JoranBeasley, actually, I meant that the TSP REQUIRES only one visit per node, which adds quite a bit of complexity to the problem – im so confused Sep 05 '12 at 16:37
  • @darksky I'm interested in this same problem. You didn't accept any answer here, so it's not clear what you ended up doing. Would you mind briefly describing what your solution was? – Jon G. Jan 26 '13 at 08:33

5 Answers5

3

That is a version of the Travelling Salesman Problem, for which the wikipedia article has good overviews of various different heuristics.

The big difference between standard TSP and your algorithm is that TSP normally enforces only one visit per node, whereas you are allowing multiple visits. That problem was answered nicely in this SO question.

This guy documented his Python TSP solution, and this a pretty helpful discussion of generally how to implement graph stuff in Python.

Community
  • 1
  • 1
chm
  • 1,519
  • 13
  • 21
2

Single-Source-Shortest-Path

If you have a node $s$ and want to find to some shortest path to a node $t$.

If the graph has non-negative edge weights, Dijkstra's Algorithm will find the optimal answer in time $O(|E| + |V|\log |V|)$.

However, if the graph contains negative edge weights, Bellman-Ford's Algorithm will find the optimal answer in $O(|V||E|)$ time, subject to the constraint that the graph does not contain negative-weight cycles.

All-Pairs-Shortest-Path

This is to find the shortest path between any two nodes $u,v$ in the graph. It can be solved by Floyd-Warshall's Algorithm in time $O(|V|^3).$ Similarly to the Bellman-Ford approach, the graph must not contain negative-weight cycles.

The reasoning for the negative-weight cycle constraint is that a shortest path could continually take the cycle and reduce its weight (as shown below).

enter image description here

Community
  • 1
  • 1
Ravindra Bagale
  • 17,226
  • 9
  • 43
  • 70
  • Thanks. This is a good point. Of course, the weights are are non-negative. But it actually looks like Bellman-Ford's Algorithm gives the shortest path from any arbitrary node to all nodes, similar to Dijkstra's algorithm. – darksky Sep 30 '12 at 22:20
1

Use Iterative Limited Depth First Search

see

http://en.wikipedia.org/wiki/Depth-limited_search

Joran Beasley
  • 110,522
  • 12
  • 160
  • 179
1

A simple approach is to build the minimum spanning tree for your graph and do a (depth-first) walk over it, skipping nodes already visited.

This is proven to be no more than twice as long as the optimal TSP path. You can definitely do better with heuristics, but it's a starter (and easy to implement too).

Kos
  • 70,399
  • 25
  • 169
  • 233
  • minimum spanning tree sounds like a very useful tool. In general, twice as long as optimal path is pretty bad, but I hope I can get somewhere with this. – darksky Sep 30 '12 at 22:22
0

EDIT 3: Nope, still looking

EDIT 2:

Here we go darksky, it has been way too long since i've done this haha

Djikstra's Algorithm

D's Algorithm finds the shortest distance from your starting node and every other node in a graph.

Here is a python implementation that looks reasonable to modify to work with your code:

Python Implementation

EDIT: As correctly pointed out in the comments, A* is (in one iteration) used for a single path. As such your requirement of visiting each node once is not met. I still think TSP is a much more complicated problem than the one you face as you are allowed to visit nodes > 1 time.

Original: A*

A* Wiki Article

I loved solving this problem back in college, enjoy!

im so confused
  • 2,091
  • 1
  • 16
  • 25
  • not sure this is good since it doesnt necesarilly visit each node..its fine for pathfinding but if you really want to visit each node thats the traveling salesman and afaik A* doesnt really help – Joran Beasley Sep 05 '12 at 16:33
  • Hm excellent point, did not read thoroughly. Are you thinking Djikstra's or Prim's then? – im so confused Sep 05 '12 at 16:34
  • Im not sure I cant remember how I solved back in that class ... but I remember it was basically brute forcing all possible paths – Joran Beasley Sep 05 '12 at 16:37
  • I can indeed write a A* algorithm to traverse the graph. But that is begging the question: What heuristic would you use to guide the A*? – darksky Sep 05 '12 at 16:37
  • you cant i dont think use A* to guarantee visiting all nodes ... if im wrong please point me in the right direction it just finds the lowest cost path between 2 points ... you could repeat it ad nauseum i guess where the target was always one of your neighbors ... but I think you lose all of A*'s efficiency doing that – Joran Beasley Sep 05 '12 at 16:38
  • I'm pretty certain you can. It's just that the goal-test of the search problem is "check every node and see if they are visited". That can be done with some simple bookkeeping. So his answer is not wrong. – darksky Sep 05 '12 at 16:40
  • @darksky I don't think A* would be the best solution here as the comments and edits explain. I think a "filling" algorithm is the required solution. IE from start node, check all the nearest, but least cost first. Let me google a bit for the name of the algorithm. For some reason Djikstra and Prim come to mind – im so confused Sep 05 '12 at 16:40
  • @darksky yes you are correct, A* can be modified to solve your problem by pathfinding to each node of course, but I think there is a better solution, to try to answer your "as optimal as possible" part – im so confused Sep 05 '12 at 16:41
  • @AkshayaAnnavajhala yes exactly. A* without a heuristic is just a uniform-cost-search. It will work, but it's darn slow. – darksky Sep 05 '12 at 16:42
  • @darksky please see the edit above. That, I'm confident, is the answer you are looking for, and i'm positive python implementations abound – im so confused Sep 05 '12 at 16:44
  • 1
    @AkshayaAnnavajhala But read in the page you cited: "Dijkstra(G,s) finds all shortest paths from s to each other vertex in the graph," that is from S to A, from S to B, and so on... This is different that from S to A to B back to A now to C etc. – darksky Sep 05 '12 at 16:50
  • @darksky you know, there's a reason most people that stay in touch with these subjects are the ones that are still good :D you are of course correct. excuse my brain. I'll try to legitimately answer your question later after a couple coffees – im so confused Sep 05 '12 at 16:55
  • @darksky Before I triumphantly announce the second coming (more like 3rd in this case), look at this: http://en.wikipedia.org/wiki/Prim%27s_algorithm – im so confused Sep 05 '12 at 16:56
  • @AkshayaAnnavajhala No worries! Don't feel bad. Thanks for trying anyway. I'll take a look at your other link. – darksky Sep 05 '12 at 17:11
  • @darksky After more research I think your problem relates most closely to the Longest Path Problem, an NP-complete problem. While I think your problem is not the TSP due to the relaxation of visit-only-once rule (which intuitively made it easier in my mind), you may be stuck with the same NP-hardness of the TSP. That would require much more than a simple wiki article to analyze, and I'll take a look at it tonight on my precious whiteboard ;) – im so confused Sep 05 '12 at 17:20
  • 1
    iterative limited depth first search is what you want :) – Joran Beasley Sep 05 '12 at 18:09
  • @JoranBeasley and mark a path complete when one of its paths contains all the nodes? I like this. Seems extremely promising!"It is optimal when the path cost is a non-decreasing function of the depth of the node." Seems like this may or may not be necessarily true, but I think this is the best answer yet – im so confused Sep 05 '12 at 19:56
  • Im pretty sure it fits this problem criteria ... basically as long as there are no negative weight edges it should be a non-decreasing function of depth ... so it should(will) find the optimal route – Joran Beasley Sep 05 '12 at 20:39