Plane fitting to 4 (or more) XYZ points

Question

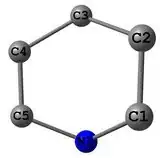
I have 4 points, which are very near to be at the one plane - it is the 1,4-Dihydropyridine cycle.

I need to calculate distance from C3 and N1 to the plane, which is made of C1-C2-C4-C5. Calculating distance is OK, but fitting plane is quite difficult to me.

1,4-DHP cycle:

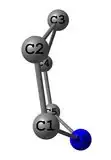
1,4-DHP cycle, another view:

from array import *
from numpy import *
from scipy import *

# coordinates (XYZ) of C1, C2, C4 and C5
x = [0.274791784, -1.001679346, -1.851320839, 0.365840754]
y = [-1.155674199, -1.215133985, 0.053119249, 1.162878076]
z = [1.216239624, 0.764265677, 0.956099579, 1.198231236]

# plane equation Ax + By + Cz = D
# non-fitted plane
abcd = [0.506645455682, -0.185724560275, -1.43998120646, 1.37626378129]

# creating distance variable
distance =  zeros(4, float)

# calculating distance from point to plane
for i in range(4):
    distance[i] = (x[i]*abcd[0]+y[i]*abcd[1]+z[i]*abcd[2]+abcd[3])/sqrt(abcd[0]**2 + abcd[1]**2 + abcd[2]**2)
    
print distance

# calculating squares
squares = distance**2

print squares

How to make sum(squares) minimized? I have tried least squares, but it is too hard for me.

Answer 1

That sounds about right, but you should replace the nonlinear optimization with an SVD. The following creates the moment of inertia tensor, M, and then SVD's it to get the normal to the plane. This should be a close approximation to the least-squares fit and be much faster and more predictable. It returns the point-cloud center and the normal.

def planeFit(points):
    """
    p, n = planeFit(points)

    Given an array, points, of shape (d,...)
    representing points in d-dimensional space,
    fit an d-dimensional plane to the points.
    Return a point, p, on the plane (the point-cloud centroid),
    and the normal, n.
    """
    import numpy as np
    from numpy.linalg import svd
    points = np.reshape(points, (np.shape(points)[0], -1)) # Collapse trialing dimensions
    assert points.shape[0] <= points.shape[1], "There are only {} points in {} dimensions.".format(points.shape[1], points.shape[0])
    ctr = points.mean(axis=1)
    x = points - ctr[:,np.newaxis]
    M = np.dot(x, x.T) # Could also use np.cov(x) here.
    return ctr, svd(M)[0][:,-1]

For example: Construct a 2D cloud at (10, 100) that is thin in the x direction and 100 times bigger in the y direction:

>>> pts = np.diag((.1, 10)).dot(randn(2,1000)) + np.reshape((10, 100),(2,-1))

The fit plane is very nearly at (10, 100) with a normal very nearly along the x axis.

>>> planeFit(pts)

    (array([ 10.00382471,  99.48404676]),
     array([  9.99999881e-01,   4.88824145e-04]))

Answer 2

Least squares should fit a plane easily. The equation for a plane is: ax + by + c = z. So set up matrices like this with all your data:

    x_0   y_0   1  
A = x_1   y_1   1  
          ... 
    x_n   y_n   1  

And

    a  
x = b  
    c

And

    z_0   
B = z_1   
    ...   
    z_n

In other words: Ax = B. Now solve for x which are your coefficients. But since you have more than 3 points, the system is over-determined so you need to use the left pseudo inverse. So the answer is:

a 
b = (A^T A)^-1 A^T B
c

And here is some simple Python code with an example:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

N_POINTS = 10
TARGET_X_SLOPE = 2
TARGET_y_SLOPE = 3
TARGET_OFFSET  = 5
EXTENTS = 5
NOISE = 5

# create random data
xs = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
ys = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
zs = []
for i in range(N_POINTS):
    zs.append(xs[i]*TARGET_X_SLOPE + \
              ys[i]*TARGET_y_SLOPE + \
              TARGET_OFFSET + np.random.normal(scale=NOISE))

# plot raw data
plt.figure()
ax = plt.subplot(111, projection='3d')
ax.scatter(xs, ys, zs, color='b')

# do fit
tmp_A = []
tmp_b = []
for i in range(len(xs)):
    tmp_A.append([xs[i], ys[i], 1])
    tmp_b.append(zs[i])
b = np.matrix(tmp_b).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * b
errors = b - A * fit
residual = np.linalg.norm(errors)

print("solution: %f x + %f y + %f = z" % (fit[0], fit[1], fit[2]))
print("errors:")
print(errors)
print("residual: {}".format(residual))

# plot plane
xlim = ax.get_xlim()
ylim = ax.get_ylim()
X,Y = np.meshgrid(np.arange(xlim[0], xlim[1]),
                  np.arange(ylim[0], ylim[1]))
Z = np.zeros(X.shape)
for r in range(X.shape[0]):
    for c in range(X.shape[1]):
        Z[r,c] = fit[0] * X[r,c] + fit[1] * Y[r,c] + fit[2]
ax.plot_wireframe(X,Y,Z, color='k')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

The solution for your points:

0.143509 x + 0.057196 y + 1.129595 = z

Answer 3

The fact that you are fitting to a plane is only slightly relevant here. What you are trying to do is minimize a particular function starting from a guess. For that use scipy.optimize. Note that there is no guarantee that this is the globally optimal solution, only locally optimal. A different initial condition may converge to a different result, this works well if you start close to the local minima you are seeking.

I've taken the liberty to clean up your code by taking advantage of numpy's broadcasting:

import numpy as np

# coordinates (XYZ) of C1, C2, C4 and C5
XYZ = np.array([
        [0.274791784, -1.001679346, -1.851320839, 0.365840754],
        [-1.155674199, -1.215133985, 0.053119249, 1.162878076],
        [1.216239624, 0.764265677, 0.956099579, 1.198231236]])

# Inital guess of the plane
p0 = [0.506645455682, -0.185724560275, -1.43998120646, 1.37626378129]

def f_min(X,p):
    plane_xyz = p[0:3]
    distance = (plane_xyz*X.T).sum(axis=1) + p[3]
    return distance / np.linalg.norm(plane_xyz)

def residuals(params, signal, X):
    return f_min(X, params)

from scipy.optimize import leastsq
sol = leastsq(residuals, p0, args=(None, XYZ))[0]

print("Solution: ", sol)
print("Old Error: ", (f_min(XYZ, p0)**2).sum())
print("New Error: ", (f_min(XYZ, sol)**2).sum())

This gives:

Solution:  [  14.74286241    5.84070802 -101.4155017   114.6745077 ]
Old Error:  0.441513295404
New Error:  0.0453564286112

Answer 4

This returns the 3D plane coefficients along with the RMSE of the fit.

The plane is provided in a homogeneous coordinate representation, meaning its dot product with the homogeneous coordinates of a point produces the distance between the two.

def fit_plane(points):
    assert points.shape[1] == 3
    centroid = points.mean(axis=0)
    x = points - centroid[None, :]
    U, S, Vt = np.linalg.svd(x.T @ x)
    normal = U[:, -1]
    origin_distance = normal @ centroid
    rmse = np.sqrt(S[-1] / len(points))
    return np.hstack([normal, -origin_distance]), rmse

Minor note: the SVD can also be directly applied to the points instead of the outer product matrix, but I found it to be slower with NumPy's SVD implementation.

U, S, Vt = np.linalg.svd(x.T, full_matrices=False)
rmse = S[-1] / np.sqrt(len(points))

Answer 5

Another way aside from svd to quickly reach a solution while dealing with outliers ( when you have a large data set ) is ransac :

def fit_plane(voxels, iterations=50, inlier_thresh=10):  # voxels : x,y,z
    inliers, planes = [], []
    xy1 = np.concatenate([voxels[:, :-1], np.ones((voxels.shape[0], 1))], axis=1)
    z = voxels[:, -1].reshape(-1, 1)
    for _ in range(iterations):
        random_pts = voxels[np.random.choice(voxels.shape[0], voxels.shape[1] * 10, replace=False), :]
        plane_transformation, residual = fit_pts_to_plane(random_pts)
        inliers.append(((z - np.matmul(xy1, plane_transformation)) <= inlier_thresh).sum())
        planes.append(plane_transformation)
    return planes[np.array(inliers).argmax()]


def fit_pts_to_plane(voxels):  # x y z  (m x 3)
    # https://math.stackexchange.com/questions/99299/best-fitting-plane-given-a-set-of-points
    xy1 = np.concatenate([voxels[:, :-1], np.ones((voxels.shape[0], 1))], axis=1)
    z = voxels[:, -1].reshape(-1, 1)
    fit = np.matmul(np.matmul(np.linalg.inv(np.matmul(xy1.T, xy1)), xy1.T), z)
    errors = z - np.matmul(xy1, fit)
    residual = np.linalg.norm(errors)
    return fit, residual

Answer 6

Here's one way. If your points are P[1]..P[n] then compute the mean M of these and subtract it from each, getting points p[1]..p[n]. Then compute C = Sum{ p[i]*p[i]'} (the "covariance" matrix of the points). Next diagonalise C, that is find orthogonal U and diagonal E so that C = U*E*U'. If your points are indeed on a plane then one of the eigenvalues (ie the diagonal entries of E) will be very small (with perfect arithmetic it would be 0). In any case if the j'th one of these is the smallest, then let the j'th column of U be (A,B,C) and compute D = -M'*N. These parameters define the "best" plane, the one such that the sum of the squares of the distances from the P[] to the plane is least.