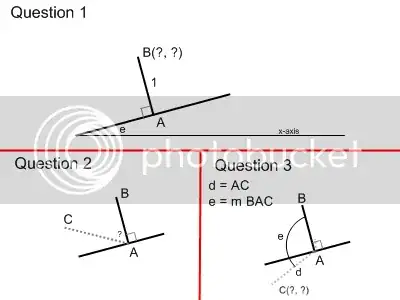
I actually have two questions, I found the answer to the second and didn't update the diagram. I'm not actually sure if these are possible, they really stumped me.
Question 1: Given point A and e, the angle of the line A is on relative to the x-axis where 0<=e<360 degrees, how do you calculate the coordinates of B? BA is perpendicular to A's line and 1 unit long.
SOLVED: I start by taking the unit vector from a parallel to the x-axis and then I rotate it 90 + e degrees.
Question 2: I'm using this approach. If anyone has any better suggestions, please let me know.
SOLVED: I find the dot product of the vector from step 1 and the normalized vector AC.
Question 3: This one should be pretty self-explanatory from the diagram. I need to find the coordinates of C given A, B, the angle of BAC and the distance between A and C.
SOLVED: I rotate BA e degrees and then change the magnitude to d.
If anyone spots problems with my solutions, please comment.