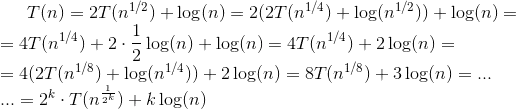7

I am trying to find the time complexity for the recurrence:

T(n) = 2T(n1/2) + log n

I am pretty close to the solution, however, I have run into a roadblock. I need to solve:

n(1/2k) = 1

for k to simplify my substitution pattern. I am not looking for answers to the recurrence, just a solution for k.

Community
  • 1
  • 1
Waqas
  • 311
  • 1
  • 3
  • 10
  • I don't think that would help. If you solve that for `k` you get something positively frightening. – harold Oct 27 '12 at 20:39
  • 1
    I'm voting to close this question as off-topic because it is a mathematics question, not a programming question. – Raymond Chen Sep 18 '18 at 01:54
  • 2
    Stack Overflow is a site for programming and development questions. This question appears to be off-topic because it is not about programming or development. See [What topics can I ask about here](http://stackoverflow.com/help/on-topic) in the Help Center. Perhaps [Mathematics Stack Exchange](http://math.stackexchange.com/) would be a better place to ask. – jww Sep 18 '18 at 03:19

4 Answers4

7

When you start unrolling the recursion, you get: enter image description here

Here the same thing with a few additional steps:

enter image description here

Now using the boundary condition for a recursion (number 2 selected as 0 and 1 do not make sense), you will get:

enter image description here

Substituting k back to the equation you will get:

enter image description here

Here are a couple of recursions that use the same idea.

Salvador Dali
  • 214,103
  • 147
  • 703
  • 753
3

It's impossible to solve

n(1/2k) = 1

for k, since if n > 1 then nx > 1 for any nonzero x. The only way that you could solve this is if you picked k such that 1 / 2k = 0, but that's impossible.

However, you can solve this:

n(1/2k) = 2

First, take the log of both sides:

(1 / 2k) lg n = lg 2 = 1

Next, multiply both sides by 2k:

lg n = 2k

Finally, take the log one more time:

lg lg n = k

Therefore, this recurrence will stop once k = lg lg n.

Although you only asked for the value of k, since it's been a full year since you asked, I thought I'd point out that you can do a variable substitution to solve this problem. Try setting k = 2n. Then k = lg n, so your recurrence is

T(k) = 2T(k / 2) + k

This solves (using the Master Theorem) to T(k) = Θ(k log k), and using the fact that k = lg n, the overall recurrence solves to Θ(log n log log n).

Hope this helps!

templatetypedef
  • 362,284
  • 104
  • 897
  • 1,065
  • sir, can i solve it like this -:T(n) = 2T(n1/2) + log n =>T(2^m)=2T(2^(m/2))+log 2^m =>T(2^m)=2T(2^(m/2))+m=>let 2^m=k=>S(k)=2S(k/2)+log k – laura Sep 13 '17 at 12:14
  • 1
    Close! If you plug in k = 2^n, what happens to the log n term when you express it as a function of k? – templatetypedef Sep 13 '17 at 20:19
0

dude if it were quick sort that was the equation:

enter image description here

The solution for this is O(n*log(n)) since now it is even smaller(T(n) ~ n^1/2) for some N it means your complexity is less than O(n*log(n)).

Try to use induction to prove your bound

0x90
  • 39,472
  • 36
  • 165
  • 245
  • Yeah, I agree it would be, as the combine is sub linear, and the input size is much smaller as well. However, if all else fails, I will try induction, but I am just curious in general how I might solve equations of the form c^a^b = 1 for b. I know it involves some trickery using power identities. – Waqas Oct 27 '12 at 20:42
0

log base anything of 1, is 0.

so

n^((1/2)^k) = 1

log(n)(n^((1/2)^k)) = log(n)(1)

1/2^k = 0

log(1/2)((1/2)^k) = log(1/2)(0)

log base anything of 0 is negative infinity.. so...

k = -infinity.

I think you should use a different "final number" for n, than 1 just saying...

Serge
  • 1,974
  • 6
  • 21
  • 33
  • mainly because you'll never be able to continue square rooting until 1. You'll go insane. – Serge Oct 27 '12 at 20:54