There are several different methods for converting floating point numbers to Integers in JavaScript. My question is what method gives the best performance, is most compatible, or is considered the best practice?
Here are a few methods that I know of:
var a = 2.5;
window.parseInt(a); // 2
Math.floor(a); // 2
a | 0; // 2
I'm sure there are others out there. Suggestions?
According to this website:
parseInt is occasionally used as a means of turning a floating point number into an integer. It is very ill suited to that task because if its argument is of numeric type it will first be converted into a string and then parsed as a number...
For rounding numbers to integers one of Math.round, Math.ceil and Math.floor are preferable...
Apparently double bitwise-not is the fastest way to floor a number:
var x = 2.5;
console.log(~~x); // 2
Used to be an article here, getting a 404 now though: http://james.padolsey.com/javascript/double-bitwise-not/
Google has it cached: http://74.125.155.132/search?q=cache:wpZnhsbJGt0J:james.padolsey.com/javascript/double-bitwise-not/+double+bitwise+not&cd=1&hl=en&ct=clnk&gl=us
But the Wayback Machine saves the day! http://web.archive.org/web/20100422040551/http://james.padolsey.com/javascript/double-bitwise-not/
From "Javascript: The Good Parts" from Douglas Crockford:
Number.prototype.integer = function () {
return Math[this < 0 ? 'ceil' : 'floor'](this);
}
Doing that your are adding a method to every Number object.
Then you can use it like that:
var x = 1.2, y = -1.2;
x.integer(); // 1
y.integer(); // -1
(-10 / 3).integer(); // -3
The 'best' way depends on:
float | trunc | floor | ceil | near (half up) ------+-------+-------+-------+--------------- +∞ | +∞ | +∞ | +∞ | +∞ +2.75 | +2 | +2 | +3 | +3 +2.5 | +2 | +2 | +3 | +3 +2.25 | +2 | +2 | +3 | +2 +0 | +0 | +0 | +0 | +0 NaN | NaN | NaN | NaN | NaN -0 | -0 | -0 | -0 | -0 -2.25 | -2 | -3 | -2 | -2 -2.5 | -2 | -3 | -2 | -2 -2.75 | -2 | -3 | -2 | -3 -∞ | -∞ | -∞ | -∞ | -∞For float to integer conversions we commonly expect "truncation"
StringNumberString (default radix 10) (on screen) Only after these considerations are answered we can think about appropriate method(s) and speed!
Number) in javascript are represented/stored in:As this format stores 1 sign bit, 11 exponent bits and the first 53 significant bits ("mantissa"), we can say that: only Number-values between -252 and +252 can have a fraction.
In other words: all representable positive and negative Number-values between 252 to (almost) 2(211/2=1024) (at which point the format calls it a day Infinity) are already integers (internally rounded, as there are no bits left to represent the remaining fractional and/or least significant integer digits).
And there is the first 'gotcha':
You can not control the internal rounding-mode of Number-results for the built-in Literal/String to float conversions (rounding-mode: IEEE 754-2008 "round to nearest, ties to even") and built-in arithmetic operations (rounding-mode: IEEE 754-2008 "round-to-nearest").
For example:
252+0.25 = 4503599627370496.25 is rounded and stored as: 4503599627370496
252+0.50 = 4503599627370496.50 is rounded and stored as: 4503599627370496
252+0.75 = 4503599627370496.75 is rounded and stored as: 4503599627370497
252+1.25 = 4503599627370497.25 is rounded and stored as: 4503599627370497
252+1.50 = 4503599627370497.50 is rounded and stored as: 4503599627370498
252+1.75 = 4503599627370497.75 is rounded and stored as: 4503599627370498
252+2.50 = 4503599627370498.50 is rounded and stored as: 4503599627370498
252+3.50 = 4503599627370499.50 is rounded and stored as: 4503599627370500
To control rounding your Number needs a fractional part (and at least one bit to represent that), otherwise ceil/floor/trunc/near returns the integer you fed into it.
To correctly ceil/floor/trunc a Number up to x significant fractional decimal digit(s), we only care if the corresponding lowest and highest decimal fractional value will still give us a binary fractional value after rounding (so not being ceiled or floored to the next integer).
So, for example, if you expect 'correct' rounding (for ceil/floor/trunc) up to 1 significant fractional decimal digit (x.1 to x.9), we need at least 3 bits (not 4) to give us a binary fractional value:
0.1 is closer to 1/(23=8)=0.125 than it is to 0 and 0.9 is closer to 1-1/(23=8)=0.875 than it is to 1.
only up to ±2(53-3=50) will all representable values have a non-zero binary fraction for no more than the first significant decimal fractional digit (values x.1 to x.9).
For 2 decimals ±2(53-6=47), for 3 decimals ±2(53-9=44), for 4 decimals ±2(53-13=40), for 5 decimals ±2(53-16=37), for 6 decimals ±2(53-19=34), for 7 decimals ±2(53-23=30), for 8 decimals ±2(53-26=27), for 9 decimals ±2(53-29=24), for 10 decimals ±2(53-33=20), for 11 decimals ±2(53-36=17), etc..
A "Safe Integer" in javascript is an integer:
±253 (as an exact power of 2) can exactly be represented, it is not a safe integer because it could also have been ±(253+1) before it was rounded to fit into the maximum of 53 most significant bits).This effectively defines a subset range of (safely representable) integers between -253 and +253:
-(253 - 1) = -9007199254740991 (inclusive)Number.MIN_SAFE_INTEGER since ES6)to: +(253 - 1) = +9007199254740991 (inclusive)
(a constant provided as static property Number.MAX_SAFE_INTEGER since ES6)
Trivial polyfill for these 2 new ES6 constants:
Number.MIN_SAFE_INTEGER || (Number.MIN_SAFE_INTEGER=
-(Number.MAX_SAFE_INTEGER=9007199254740991) //Math.pow(2,53)-1
);
Since ES6 there is also a complimentary static method Number.isSafeInteger() which tests if the passed value is of type Number and is an integer within the safe integer range (returning a boolean true or false).
Note: will also return false for: NaN, Infinity and obviously String (even if it represents a number).
Polyfill example:
Number.isSafeInteger || (Number.isSafeInteger = function(value){
return typeof value === 'number' &&
value === Math.floor(value) &&
value < 9007199254740992 &&
value > -9007199254740992;
});
ECMAScript 2015 / ES6 provides a new static method Math.trunc()
to truncate a float to an integer:
Returns the integral part of the number x, removing any fractional digits. If x is already an integer, the result is x.
Or put simpler (MDN):
Unlike other three Math methods:
Math.floor(),Math.ceil()andMath.round(), the wayMath.trunc()works is very simple and straightforward:
just truncate the dot and the digits behind it, no matter whether the argument is a positive number or a negative number.
We can further explain (and polyfill) Math.trunc() as such:
Math.trunc || (Math.trunc = function(n){
return n < 0 ? Math.ceil(n) : Math.floor(n);
});
Note, the above polyfill's payload can potentially be better pre-optimized by the engine compared to:
Math[n < 0 ? 'ceil' : 'floor'](n);
Usage: Math.trunc(/* Number or String */)
Input: (Integer or Floating Point) Number (but will happily try to convert a String to a Number)
Output: (Integer) Number (but will happily try to convert Number to String in a string-context)
Range: -2^52 to +2^52 (beyond this we should expect 'rounding-errors' (and at some point scientific/exponential notation) plain and simply because our Number input in IEEE 754 already lost fractional precision: since Numbers between ±2^52 to ±2^53 are already internally rounded integers (for example 4503599627370509.5 is internally already represented as 4503599627370510) and beyond ±2^53 the integers also loose precision (powers of 2)).
Float to integer conversion by subtracting the Remainder (%) of a devision by 1:
Example: result = n-n%1 (or n-=n%1)
This should also truncate floats. Since the Remainder operator has a higher precedence than Subtraction we effectively get: (n)-(n%1).
For positive Numbers it's easy to see that this floors the value: (2.5) - (0.5) = 2,
for negative Numbers this ceils the value: (-2.5) - (-0.5) = -2 (because --=+ so (-2.5) + (0.5) = -2).
Since the input and output are Number we should get the same useful range and output compared to ES6 Math.trunc() (or it's polyfill).
Note: tough I fear (not sure) there might be differences: because we are doing arithmetic (which internally uses rounding mode "nearTiesEven" (aka Banker's Rounding)) on the original Number (the float) and a second derived Number (the fraction) this seems to invite compounding digital_representation and arithmetic rounding errors, thus potentially returning a float after all..
Float to integer conversion by (ab-)using bitwise operations:
This works by internally forcing a (floating point) Number conversion (truncation and overflow) to a signed 32-bit integer value (two's complement) by using a bitwise operation on a Number (and the result is converted back to a (floating point) Number which holds just the integer value).
Again, input and output is Number (and again silent conversion from String-input to Number and Number-output to String).
More important tough (and usually forgotten and not explained):
depending on bitwise operation and the number's sign, the useful range will be limited between:
-2^31 to +2^31 (like ~~num or num|0 or num>>0) OR 0 to +2^32 (num>>>0).
This should be further clarified by the following lookup-table (containing all 'critical' examples):
n | n>>0 OR n<<0 OR | n>>>0 | n < 0 ? -(-n>>>0) : n>>>0
| n|0 OR n^0 OR ~~n | |
| OR n&0xffffffff | |
----------------------------+-------------------+-------------+---------------------------
+4294967298.5 = (+2^32)+2.5 | +2 | +2 | +2
+4294967297.5 = (+2^32)+1.5 | +1 | +1 | +1
+4294967296.5 = (+2^32)+0.5 | 0 | 0 | 0
+4294967296 = (+2^32) | 0 | 0 | 0
+4294967295.5 = (+2^32)-0.5 | -1 | +4294967295 | +4294967295
+4294967294.5 = (+2^32)-1.5 | -2 | +4294967294 | +4294967294
etc... | etc... | etc... | etc...
+2147483649.5 = (+2^31)+1.5 | -2147483647 | +2147483649 | +2147483649
+2147483648.5 = (+2^31)+0.5 | -2147483648 | +2147483648 | +2147483648
+2147483648 = (+2^31) | -2147483648 | +2147483648 | +2147483648
+2147483647.5 = (+2^31)-0.5 | +2147483647 | +2147483647 | +2147483647
+2147483646.5 = (+2^31)-1.5 | +2147483646 | +2147483646 | +2147483646
etc... | etc... | etc... | etc...
+1.5 | +1 | +1 | +1
+0.5 | 0 | 0 | 0
0 | 0 | 0 | 0
-0.5 | 0 | 0 | 0
-1.5 | -1 | +4294967295 | -1
etc... | etc... | etc... | etc...
-2147483646.5 = (-2^31)+1.5 | -2147483646 | +2147483650 | -2147483646
-2147483647.5 = (-2^31)+0.5 | -2147483647 | +2147483649 | -2147483647
-2147483648 = (-2^31) | -2147483648 | +2147483648 | -2147483648
-2147483648.5 = (-2^31)-0.5 | -2147483648 | +2147483648 | -2147483648
-2147483649.5 = (-2^31)-1.5 | +2147483647 | +2147483647 | -2147483649
-2147483650.5 = (-2^31)-2.5 | +2147483646 | +2147483646 | -2147483650
etc... | etc... | etc... | etc...
-4294967294.5 = (-2^32)+1.5 | +2 | +2 | -4294967294
-4294967295.5 = (-2^32)+0.5 | +1 | +1 | -4294967295
-4294967296 = (-2^32) | 0 | 0 | 0
-4294967296.5 = (-2^32)-0.5 | 0 | 0 | 0
-4294967297.5 = (-2^32)-1.5 | -1 | +4294967295 | -1
-4294967298.5 = (-2^32)-2.5 | -2 | +4294967294 | -2
Note 1: the last column has extended range 0 to -4294967295 using (n < 0 ? -(-n>>>0) : n>>>0).
Note 2: bitwise introduces its own conversion-overhead(s) (severity vs Math depends on actual implementation, so bitwise could be faster (often on older historic browsers)).
String to begin with,parseInt(/*String*/, /*Radix*/) would be an appropriate choice to parse it into a integer Number.parseInt() will truncate as well (for positive and negative numbers).Math method(s).
Finally, if you have a String and expect a String as output you could also chop of the radix point and fraction (which also gives you a larger accurate truncation range compared to IEEE 754 double precision floating point (±2^52))!
If for example you'd want round away from zero (aka round towards infinity) you could modify the Math.trunc() polyfill, for example:
Math.intToInf || (Math.intToInf = function(n){
return n < 0 ? Math.floor(n) : Math.ceil(n);
});
The answer has already been given but just to be clear.
Use the Math library for this. round, ceil or floor functions.
parseInt is for converting a string to an int which is not what is needed here
toFixed is for converting a float to a string also not what is needed here
Since the Math functions will not be doing any conversions to or from a string it will be faster than any of the other choices which are wrong anyway.
You can use Number(a).toFixed(0);
Or even just a.toFixed(0);
Edit:
That's rounding to 0 places, slightly different than truncating, and as someone else suggested, toFixed returns a string, not a raw integer. Useful for display purposes.
var num = 2.7; // typeof num is "Number"
num.toFixed(0) == "3"
var i = parseInt(n, 10);
If you don't specify a radix values like '010' will be treated as octal (and so the result will be 8 not 10).
So I made a benchmark, on Chrome when the input is already a number, the fastest would be ~~num and num|0, half speed: Math.floor, and the slowest would be parseInt see here
EDIT: it seems there are already another person who made rounding benchmark (more result) and additional ways: num>>0 (as fast as |0) and num - num%1 (sometimes fast)
Using bitwise operators. It may not be the clearest way of converting to an integer, but it works on any kind of datatype.
Suppose your function takes an argument value, and the function works in such a way that value must always be an integer (and 0 is accepted). Then any of the following will assign value as an integer:
value = ~~(value)
value = value | 0;
value = value & 0xFF; // one byte; use this if you want to limit the integer to
// a predefined number of bits/bytes
The best part is that this works with strings (what you might get from a text input, etc) that are numbers ~~("123.45") === 123. Any non numeric values result in 0, ie,
~~(undefined) === 0
~~(NaN) === 0
~~("ABC") === 0
It does work with hexadecimal numbers as strings (with a 0x prefix)
~~("0xAF") === 175
There is some type coercion involved, I suppose. I'll do some performance tests to compare these to parseInt() and Math.floor(), but I like having the extra convenience of no Errors being thrown and getting a 0 for non-numbers
The question appears to be asking specifically about converting from a float to an int. My understanding is that the way to do this is to use toFixed. So...
var myFloat = 2.5;
var myInt = myFloat.toFixed(0);
Does anyone know if Math.floor() is more or less performant than Number.toFixed()?
you could also do it this way:
var string = '1';
var integer = a * 1;
parseInt() is probably the best one. a | 0 doesn't do what you really want (it just assigns 0 if a is an undefined or null value, which means an empty object or array passes the test), and Math.floor works by some type trickery (it basically calls parseInt() in the background).
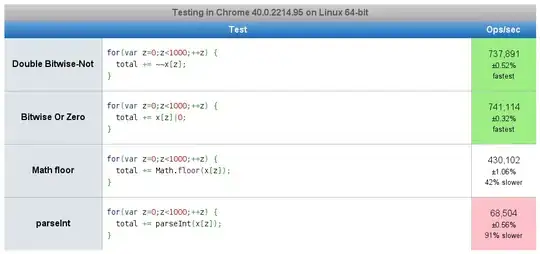
parseInt: read the original post again, carefully.ais a numeric variable, not a string. – Thomas Sep 25 '08 at 04:16