Here's visualisation of my problem.
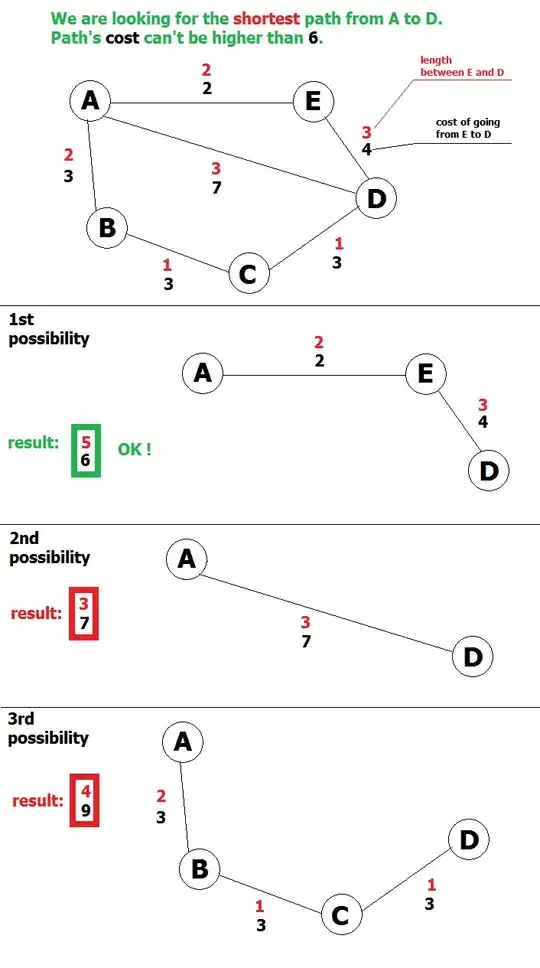
I've been trying to use djikstra on that however, It haven't worked.
Here's visualisation of my problem.

I've been trying to use djikstra on that however, It haven't worked.
The complication, as I see it, is that Dijkstra's algorithm throws away information that you need to keep around: if you are trying to get from A to E in
B
/ \
A D - E
\ /
C
And ABD is shorter than ACD, Dijkstra's will forget that ACD was ever a possibility (it uses ACD as the canonical route from A to D). But if ABD has a higher cost than ACD, and ABDE is above the quota while ACDE is below, the now eliminated ACD was correct. The problem is that Dijkstra's algorithm assumes that if one path is at least as long as another, it is weakly dominated: there is no reason to prefer it. And in one dimension of comparison, paths are weakly ordered: given any two paths, one weakly dominates the other.
But here we have two dimensions of comparison, and so ordering does not hold: one path can be shorter, the other cheaper. Since we can only discard dominated paths, we must keep all paths that do not already exceed the budget and are not dominated. I have put a bit of work into implementing this approach; it looks doable but cannot find an argument for a worst-case bound below exponential complexity (although normal performance should be much better, since in a sane graphs most paths are dominated).
You can also, as Billiska notes, use k-th shortest routes algorithms and then proceed through their results until you find one below the budget. That uses time O(m+ K*n*log(m/n)); but unless someone sees an upper bound on K such that K is guaranteed to include a path under the budget (if one exists), we need to set K to be the total number of paths, again yielding exponential complexity (although again a strategy of incrementally increasing K would likely yield a reasonable average runtime, at least if length and cost are reasonably correlated).
EDIT:
Complicating (perhaps fatally) the implementation of my proposed modification is that Dijkstra's algorithm relies on an ordering of the accessibility of nodes, such that we know that if we take the unexplored node to which we have the shortest path, we will never find a better route to it (since all other routes are already known to be longer). If that shortest route is also expensive, that need not hold; even after exploring a node, we must be prepared to update paths out of it on the basis of longer but cheaper routes into it. I suspect that this will prevent it from reaching polynomial time in the worst case.
Basically you need to find the first shortest-path, check if it works, then find the second shortest-path, check if it works, and so on...
Dijkstra's algorithm isn't designed to work with such task. And just a Google search on this new definition of the problem, I arrive at Stack Overflow question on finding kth-shortest-paths. I haven't read into it yet, so don't ask me. I hope this helps.
I think you can do it with Dijkstra, but you have to change the way you are calculating the tentative distance in each step. Instead of just taking into account the distance, consider also the cost. the new distance should be 2-d number (dist, cost), when you will choose what is the minimal distance you should take the one with minimal dist AND cost <= 6, that's it.
I hope this is correct.