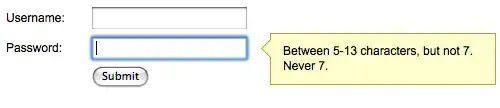
As you may have noticed by now, I keep coming back to this problem. Partly because I like to puzzle out these kinds of problems, but also because it annoyed me a little that I couldn't find an elegant algorithm for something that seems so easy.
Well, don't be fooled, this is not a trivial problem that you can solve with some simple point manipulation, although it certainly looks that way. Part of the reason for this is that, although you think you're only working with points, you're implicitly also manipulating line segments and the areas enclosed by them, which also have their own constraints (i.e. the segments should always form one or more closed chains, and cannot intersect except at the vertices we define them with).
Also, your algorithm has to work for any kind of input you feed it. That is, it is not allowed to produce no answer or a wrong answer just because the polygon you fed it is oriented in a way that your algorithm doesn't like.
What you can do however, is restrict the type of input that your algorithm accepts. Requiring that the input polygon contains only axis-aligned segments is therefore perfectly valid.
(The difference between "oriented the wrong way" and "only axis-aligned segments" is that the first is a vague criteria that cannot be determined without testing it on the algorithm - whereas the second requirement can).
To recapitulate, we're looking for a way to horizontally partition any rectilinear polygon (i.e. consisting of only axis-aligned line segments) into rectangles.
 Example of a rectilinear polygon
Example of a rectilinear polygon
Here's the plan:
- Pick our building blocks
- Allow extra vertices
- Aligning on a grid.
- Working with unequally-sized grid cells.
- Which cells are inside your polygon?
- Constructing rectangles.
Pick our building blocks
Even though these are implementation details, getting this clear up front might help you getting a better picture of how the algorithm works.
In code, we'll be using the objects of the following types as basic building blocks to represent our polygon with:
- Point, consisting of an x and y coordinate. (e.g use Point2D.Double)
- Segment, consisting of a start and end Point (e.g. use Line2D.Double)
- Polygon, consisting of a closed chain of Segments (e.g. use an ArrayList of Line2D.Double), where one segment ends on the same point as the starting point for the next segment.
Also, we'll be using a grid, which can be modelled as a 2-dimensional array.
Allow extra vertices.
You stated that "the rectangles have to be formed from using intersecting lines that start and finish on existing coordinates.". However, observe that most rectilinear polygons cannot be partitioned into rectangles by only using the existing vertices - see the example above (as well as the caravan examples you provided earlier).
Hence, this constraint will have to go - even though we won't actually be creating new vertices explicitly.
Aligning on a grid.
Thought experiment: What if your polygon existed only of (axis-aligned) segments of length 10, 20, 30 or 40... i.e. multiples of 10? We could then project our polygon on a grid, and use the grid cells that lie inside the polygon to compose the rectangles with. Also, determining the dimensions of these rectangles would be a breeze: just count the number of horizontally consecutive cells that lie inside the polygon and multiply by 10; that's your width.
 Grid-aligned polygon
Grid-aligned polygon
Good idea, except:
- The polygon doesn't consist of only segments of same-or-multiple length
- How do we determine which grid cells lie inside the polygon?
We'll tackle each of these problems next.
Working with unequally-sized grid cells.
If you think about it, there is no real reason for all the grid cells to have the same width and height. Hence, we can devise a grid that is spaced in such a way that our polygon aligns perfectly onto it.
To get the widths of the grid's horizontal axes:
- Collect all x-coordinates of the vertices of which the polygon is composed.
- De-duplicate and sort them on increasing value.
- The difference between two subsequent values then define the width of that column.
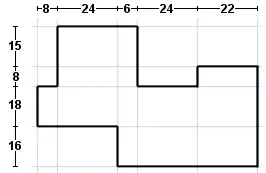 Grid aligned to the polygon
Grid aligned to the polygon
Obviously, the cell's heights can be determined in the same way. You should determine these widths and heights, and store them into two arrays called gridWidths and gridHeights, respectively.
Now that we know the number of cells and their dimensions, we can start modelling the grid contents.
Which cells are inside your polygon?
Remember that our polygon is stored as a chain of line segments. To determine if a grid cell lies inside this polygon we can use the even-odd rule: Construct a line segment from outside* the polygon to the center of the cell we want to test, and count the number of intersections between this line segment and the segments of the polygon (i.e. use Line2D.Double's intersectsLine() method). If the number is even it lies outside the polygon, if it is odd it is inside the polygon.
*- It's best to construct only horizontal line segments between center of the cells (as shown in the example), so that you don't risk intersecting the segment endpoints - this may could count as 0 or 2 intersections, messing up your count total.
So, we will model this grid as grid, a 2-dimensional array of booleans. Process each cell of the grid this way, and mark the corresponding spot in grid as either true (inside polygon) or false (outside polygon).
 Inside (T) or outside(F) based on the even-odd rule
Inside (T) or outside(F) based on the even-odd rule
Constructing rectangles.
Now that we have grid representation of the polygon, as well as the actual widths and heights of each cell, we can start constructing rectangles. I will assume that you're only interested in the widths and heights of each rectangle, and not in the actual vertex coordinates that form the rectangle (although that is now easy too).
Foreach row in grid
run_start = null
Foreach cell C in row
if C is marked as true and run_start = null
//Found the start of a new run
run_start = C
else if C is marked as false and run_start != null
//Found the end of a run
The cells [run_start...C] form a horizontal rectangle.
Use the gridWidths and gridHeights arrays to determine the
dimensions, and report this rectangle as a result
//Prepare for the next run
run_start = null
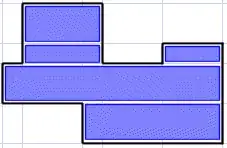 The polygon, partitioned into rectangles.
The polygon, partitioned into rectangles.
Note that the two rectangles in the top left share the same starting and ending x-coordinates, and could therefore be considered as one rectangle. If you wanted, you could implement an additional pass that merges these type of rectangles.
Conclusion
By mapping the rectilinear polygon onto a grid, we can easily partition it horizontally in rectangles without having to resort to more advanced geometric data structures.
Note that there are some optimizations possible to make this algorithm run faster, but I don't think it really matters for the current input sizes, and it would make the implementation more difficult.
 Example of a rectilinear polygon
Example of a rectilinear polygon Grid-aligned polygon
Grid-aligned polygon Grid aligned to the polygon
Grid aligned to the polygon Inside (T) or outside(F) based on the even-odd rule
Inside (T) or outside(F) based on the even-odd rule The polygon, partitioned into rectangles.
The polygon, partitioned into rectangles.