visualize error based on 2 factors

Question

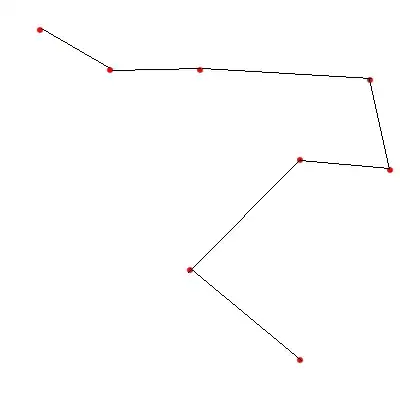
I have implemented one algorithm (RLSR) which there are two regularization factor. Based on different value of this two factors my cost function decreases or increase. Right now I visualize my error with plt.scatter by passing the error as the color which result :

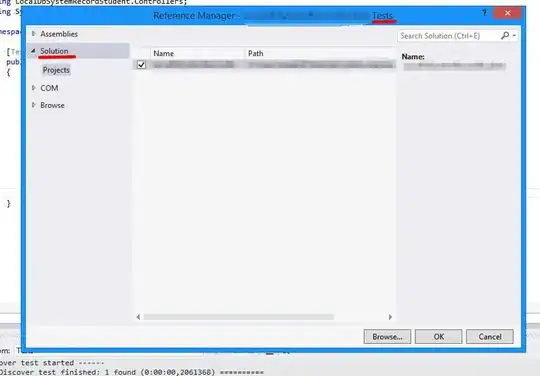
but the problem here is my values in y-axis are very small so as you can see they overlap and I can not see some part of my results.

alpha_list=[1e-11,1e-10,1e-10,5*1e-10,8*1e-10,1e-8,1e-8,5*1e-8,8*1e-6,1e-6,1e-6,5*1e-6,8*1e-6,1e-4,1e-4,5*1e-4,8*1e-4,1e-3,1e-3,5*1e-3,6*1e-3,8*1e-3]

I tried to decrease the transparency but It didn't help much!

and this is how I implemented it :

eigenvalues,alphaa  = np.meshgrid(eigRange,alpha_list )

fig = plt.figure()
DatavmaxTrain = np.max(normCostTrain)
DatavminTrain = np.min(normCostTrain)

DatavmaxTest = np.max(normCostTest)
DatavminTest = np.min(normCostTest)

plt.subplot(211)

plt.scatter(eigenvalues,alphaa,s=130, c=normCostTrain,cmap=cm.PuOr, vmin=DatavminTrain, vmax=DatavmaxTrain, alpha=0.70) #-----for train 



cb1=plt.colorbar()
cb1.set_label("normalized square error")

plt.title("Train ")
plt.xlabel("No. of Eigenvalues")
plt.ylabel("Regualrization parameter")

So I am looking for a better way to visualize my data.

Thanks

Answer 1

How about plotting the log of the alpha_list values?

alpha_list = np.log(alpha_list)

---

There is still some overlap, but at least the values are more evenly spread out:

import matplotlib.pyplot as plt
import numpy as np

alpha_list=[1e-11,1e-10,1e-10,5*1e-10,8*1e-10,1e-8,1e-8,5*1e-8,8*1e-6,1e-6,1e-6,5*1e-6,8*1e-6,1e-4,1e-4,5*1e-4,8*1e-4,1e-3,1e-3,5*1e-3,6*1e-3,8*1e-3]
alpha_list = np.log(alpha_list)
eigRange = np.linspace(0,19,20)

eigenvalues,alphaa  = np.meshgrid(eigRange,alpha_list )
normCostTrain = np.random.random((len(alpha_list),len(eigRange)))

fig = plt.figure()
DatavmaxTrain = np.max(normCostTrain)
DatavminTrain = np.min(normCostTrain)

plt.scatter(eigenvalues,alphaa,s = 130, c=normCostTrain,cmap=plt.get_cmap('PuOr'),
            vmin=DatavminTrain, vmax=DatavmaxTrain, alpha=0.70) #-----for train 

cb1=plt.colorbar()
cb1.set_label("normalized square error")

plt.title("Train ")
plt.xlabel("No. of Eigenvalues")
plt.ylabel("Log(Regularization parameter)")
plt.show()

yields

---

Here is an example of a 3D scatter plot of the same data, with the z-axis (and the color) are both used to represent the "normalized square error".

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.cm as cm
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')

alpha_list = [1e-11, 1e-10, 1e-10, 5*1e-10, 8*1e-10, 1e-8, 1e-8, 5*1e-8, 8*1e-6,
              1e-6, 1e-6, 5*1e-6, 8*1e-6, 1e-4, 1e-4, 5*1e-4, 8*1e-4, 1e-3, 1e-3,
              5*1e-3, 6*1e-3, 8*1e-3]

alpha_list = np.log(alpha_list)
eigRange = np.linspace(0, 19, 20)

eigenvalues, alphaa  = np.meshgrid(eigRange, alpha_list )
eigenvalues = eigenvalues.ravel()
alphaa = alphaa.ravel()
normCostTrain = np.random.random((len(alpha_list), len(eigRange))).ravel()

DatavmaxTrain = np.max(normCostTrain)
DatavminTrain = np.min(normCostTrain)

PuOr = plt.get_cmap('PuOr')
ax.scatter(eigenvalues, alphaa, normCostTrain,
           c = normCostTrain.ravel(),
           s = 30,
           cmap = PuOr,
           vmin = DatavminTrain,
           vmax = DatavmaxTrain,
           alpha = 0.70
           ) #-----for train

m = cm.ScalarMappable(cmap = PuOr)
m.set_array(normCostTrain)

cb1 = plt.colorbar(m)
cb1.set_label("normalized square error")

plt.title("Train ")
ax.set_xlabel("No. of Eigenvalues")
ax.set_ylabel("Log(Regularization parameter)")
ax.set_zlabel("normalized square error")
plt.show()

I'm not sure if this is an improvement. The points are a bit jumbled together, but are distinguishable if you drag the mouse to rotate the plot.