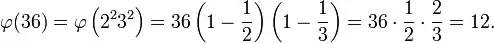I have an area of connected squares (img to the left), and want to find the maximum number of "double" squares that could be fitted into the area (img to the right).
My approach is to represent the original area as a graph, where each square represents a vertex connected by edges to the squares below, above, left and/or right.
I was thinking it could be done by using a BFS algorithm, examining each vertex and applying color. But I also have the feeling it could be done with dynamic programming... I need some help on the way!