3

I need to plot this function enter image description here

theta = (-pi:0.01:pi);
f = 3*10^9;
c = 299792458;
da = 2;

Here's my code, but I'm not sure it's correct. I dont know where exactly dot mark should be. How to set X-Axis in degress?

beta = (2*pi*f)/c;
const= (da*beta)/2; 
j= (cos(theta)+1).*(besselj(1,const*sin(theta))./(const*sin(theta)));

My another question is how to plot this function in polar coordinates.

I made something like this.

polar(theta,j);

Is it possible to rotate that function(by y-axis) to get 3D plot?

daredesm
  • 597
  • 2
  • 7
  • 22

1 Answers1

2

Things are quite right to me, although I wouldn't use the symbol j as a variable because (as i does) it is the symbol for the imaginary unit (sqrt(-1)). Doing so you are overriding it, thus things will work until you don't need complex numbers.

You should use element-wise operations such as (.*) when you aim at combining arrays entries element by element, as you correctly did to obtain F(\theta). In fact, cos(theta) is the array of the cosines of the angles contained in theta and so on.

Finally, you can rotate the plot using the command Rotate 3D in the plot window. Nonetheless, you have a 2D curve (F(\theta)) therefore, you will keep on rotating a 2D graph obtaining some kind of perspective view of it, nothing more. To obtain genuine information you need an additional dependent variable (Or I misunderstood your question?). enter image description here

EDIT: Now I see your point, you want the Surface of revolution around some axis, which I suppose by virtue of the symmetry therein to be theta=0. Well, revolution surfaces can be obtained by a bit of analytic geometry and plotted e.g. by using mesh. Check this out:

  % // 2D polar coordinate radius (your j)
  Rad= (cos(theta)+1).*(besselj(1,const*sin(theta))./(const*sin(theta)));
  Rad = abs(Rad);  % // We need its absolute value for sake of clarity


  xv = Rad .* cos(theta);  % // 2D Cartesian coordinates
  yv = Rad .* sin(theta);  % // 2D Cartesian coordinates

  phi = -pi:.01:pi;        % // 3D revolution angle around theta = 0

  % // 3D points of the surface
  xf = repmat(xv',size(phi)); 
  yf = yv' * cos(phi);
  zf = yv' * sin(phi);

  mesh(xf,yf,zf)

enter image description here

You can also add graphics effects

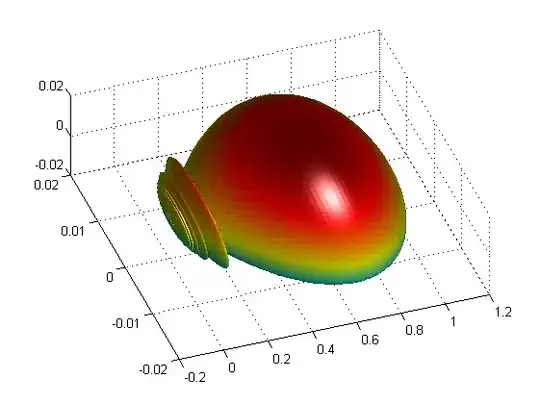
enter image description here

this is done via 

mesh(xf,yf,zf,'FaceColor','interp','FaceLighting','phong')
camlight right

and a finer angular discretization (1e-3).

Acorbe
  • 8,367
  • 5
  • 37
  • 66
  • I want to get something like this http://imageshack.us/photo/my-images/818/3dplot.png/ – daredesm Jan 05 '13 at 19:27
  • 1
    @daredesm, I got your point, around which axis do you want the revolution to be done? `theta = 0`? – Acorbe Jan 05 '13 at 19:37
  • Yes, I think theta = 0 is perfect, but is it possible to get more readable plot? – daredesm Jan 05 '13 at 20:10
  • Is it possible to get this plot without using absolute function, because I think it cut off the back shape of the plot, so is it possible to remove complex part in another way? – daredesm Jan 05 '13 at 20:22
  • @daredesm, of course, just remove it. It won't make difference indeed, though. For readability I would suggest just to plot(xv, yv), 2d but very effective. Btw you may want to consider to accept the answer by using the tick sign on the left. – Acorbe Jan 05 '13 at 20:36
  • I get error ??? Error using ==> mesh at 80 X, Y, Z, and C cannot be complex. 2D works fine, but mesh function returned error. EDIT: I think i get solution for this problem. real(argz) return real part of the complex number. – daredesm Jan 05 '13 at 20:47