6

I am doing something similar to this problem: Matching a curve pattern to the edges of an image

Basically, I have the same curve in two images, but with some affine transform between the two. Here is an example of two images:

enter image description here Image1

enter image description here Image2

So in order to get to Image2, you can apply some translation, rotation, scale, etc. to Image1.

Does anyone know how to solve for this transform?

Phase correlation doesn't work because it's not a translation only. Optical flow doesn't work since there's not enough detail to resolve translation, rotation, scale (It's pretty much a binary image). I'm not sure if Hough Transforms will give me good data.

Community
  • 1
  • 1
Jason
  • 13,563
  • 15
  • 74
  • 125
  • 1
    I would attempt using affine invariant Fourier descriptors; would skip Hough entirely; and I believe ASIFT and company are overkill for the given problem. – mmgp Jan 26 '13 at 02:15
  • Do you have other examples of curves in images that you need to match, or is this the only pair of images for which you need a solution? Some simpler techniques come to mind. Some algorithms may be overkill, as mmgp mentioned, but if an algorithm will work on this problem and can be re-used for similar problems, it may be worth having that solution ready to go. Does your image processing have to be completed within a certain period of time (10 ms, 100 ms, 1 sec)? Simulated annealing has been applied to similar problems, and worked well, but maybe that's too heavy-duty. – Rethunk Jan 26 '13 at 18:40

1 Answers1

2

I think some sort of keypoint matching algorithm like sift or surf would work with this kind of data as well. The basic idea would be to find a limited number of "interesting" keypoints in each image, then match these keypoints pairwise.

Here is a quick test of your image with an online ASIFT demo: http://demo.ipol.im/demo/my_affine_sift/result?key=BF9F4E4E006AB5168497709836C39C74#

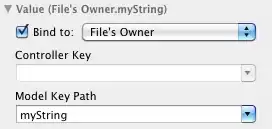
enter image description here

It is probably more suited for normal greyscale images, but nevertheless it seems to work for this data. It looks like the lines connect roughly the same points around both of the curves; plugging all these pairs into something like the FindHomography function in OpenCv, the small discrepancies should even themselves out and you get the affine transformation matrix between the two images.

For your particular data you might be able to come up with better keypoint descriptors; perhaps something to detect the line ends, line crossings and sharp corners.

Or how about this: It is a little more work, but if you can vectorize your paths into a bezier or b-spline, you can get some natural keypoints from the spline descriptors.
I do not know any vectorisation library, but Inkscape has a basic implementation with which you could test the approach. Once you have a small set of descriptors instead of a large 2d bitmap, you only need to match these descriptors between the two images, as per FindHomography.

answer to comment:

The points of interest are merely small areas that have certain properties. So the center of those areas might be black or white; the algorithm does not specifically look for white pixels or large-scale shapes such as the curve. What matter is that the lines connect roughly the same points on both curves, at least at first glance.

HugoRune
  • 13,157
  • 7
  • 69
  • 144
  • That site looks quite nice. But I can't fully understand this output, is the code drawing the lines correctly ? Or is it matching black points ? – mmgp Jan 26 '13 at 02:19
  • Well, I do not know much about this implementation myself, but I added what I know in my answer above. – HugoRune Jan 26 '13 at 10:17
  • Is it then possible to transform the first image into the second one following the calculated match? If not, is there another Algorithm/Tool which could perform this? – Samsky Apr 19 '13 at 11:57
  • 1
    @Samsky You can use openCVs FindHomography to find the best affine transformation between the two images, then use WarpAffine or WarpPerspective to transform one image into an approximation of the other. – HugoRune Apr 23 '13 at 13:52