Digitizing an analog signal

Question

I have a array of CSV values representing a digital output. It has been gathered using an analog oscilloscope so it is not a perfect digital signal. I'm trying to filter out the data to have a perfect digital signal for calculating the periods (which may vary). I would also like to define the maximum error i get from this filtration.

Something like this:

Idea

Apply a treshold od the data. Here is a pseudocode:

for data_point_raw in data_array:
    if data_point_raw < 0.8: data_point_perfect = LOW
    if data_point_raw > 2  : data_point_perfect = HIGH

else:
    #area between thresholds
    if previous_data_point_perfect == Low : data_point_perfect = LOW
    if previous_data_point_perfect == HIGH: data_point_perfect = HIGH

There are two problems bothering me.

1. This seems like a common problem in digital signal processing, however i haven't found a predefined standard function for it. Is this an ok way to perform the filtering?
2. How would I get the maximum error?

Answer 1

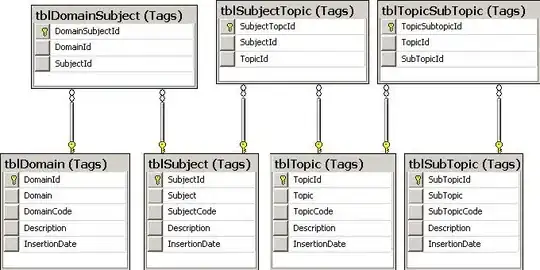
Here's a bit of code that might help.

from __future__ import division

import numpy as np


def find_transition_times(t, y, threshold):
    """
    Given the input signal `y` with samples at times `t`,
    find the times where `y` increases through the value `threshold`.

    `t` and `y` must be 1-D numpy arrays.

    Linear interpolation is used to estimate the time `t` between
    samples at which the transitions occur.
    """
    # Find where y crosses the threshold (increasing).
    lower = y < threshold
    higher = y >= threshold
    transition_indices = np.where(lower[:-1] & higher[1:])[0]

    # Linearly interpolate the time values where the transition occurs.
    t0 = t[transition_indices]
    t1 = t[transition_indices + 1]
    y0 = y[transition_indices]
    y1 = y[transition_indices + 1]
    slope = (y1 - y0) / (t1 - t0)
    transition_times = t0 + (threshold - y0) / slope

    return transition_times


def periods(t, y, threshold):
    """
    Given the input signal `y` with samples at times `t`,
    find the time periods between the times at which the
    signal `y` increases through the value `threshold`.

    `t` and `y` must be 1-D numpy arrays.
    """
    transition_times = find_transition_times(t, y, threshold)
    deltas = np.diff(transition_times)
    return deltas


if __name__ == "__main__":
    import matplotlib.pyplot as plt

    # Time samples
    t = np.linspace(0, 50, 501)
    # Use a noisy time to generate a noisy y.
    tn = t + 0.05 * np.random.rand(t.size)
    y = 0.6 * ( 1 + np.sin(tn) + (1./3) * np.sin(3*tn) + (1./5) * np.sin(5*tn) +
               (1./7) * np.sin(7*tn) + (1./9) * np.sin(9*tn))

    threshold = 0.5
    deltas = periods(t, y, threshold)
    print("Measured periods at threshold %g:" % threshold)
    print(deltas)
    print("Min:  %.5g" % deltas.min())
    print("Max:  %.5g" % deltas.max())
    print("Mean: %.5g" % deltas.mean())
    print("Std dev: %.5g" % deltas.std())

    trans_times = find_transition_times(t, y, threshold)

    plt.plot(t, y)
    plt.plot(trans_times, threshold * np.ones_like(trans_times), 'ro-')
    plt.show()

The output:

Measured periods at threshold 0.5:
[ 6.29283207  6.29118893  6.27425846  6.29580066  6.28310224  6.30335003]
Min:  6.2743
Max:  6.3034
Mean: 6.2901
Std dev: 0.0092793

You could use numpy.histogram and/or matplotlib.pyplot.hist to further analyze the array returned by periods(t, y, threshold).

Answer 2

This is not an answer for your question, just and suggestion that may help. Im writing it here because i cant put image in comment.

I think you should normalize data somehow, before any processing.

After normalization to range of 0...1 you should apply your filter.

Answer 3

If you're really only interested in the period, you could plot the Fourier Transform, you'll have a peak where the frequency of the signals occurs (and so you have the period). The wider the peak in the Fourier domain, the larger the error in your period measurement

import numpy as np

data = np.asarray(my_data)

np.fft.fft(data)

Answer 4

Your filtering is fine, it's basically the same as a schmitt trigger, but the main problem you might have with it is speed. The benefit of using Numpy is that it can be as fast as C, whereas you have to iterate once over each element.

You can achieve something similar using the median filter from SciPy. The following should achieve a similar result (and not be dependent on any magnitudes):

filtered = scipy.signal.medfilt(raw)
filtered = numpy.where(filtered > numpy.mean(filtered), 1, 0)

You can tune the strength of the median filtering with medfilt(raw, n_samples), n_samples defaults to 3.

As for the error, that's going to be very subjective. One way would be to discretise the signal without filtering and then compare for differences. For example:

discrete = numpy.where(raw > numpy.mean(raw), 1, 0)
errors = np.count_nonzero(filtered != discrete)
error_rate = errors / len(discrete)