I believe it is possible to do such a thing by creating a function for custom model formulation and its gradient. The standard SSlogis function uses a logistic function of the following form:
f(input) = Asym/(1+exp((xmid-input)/scal)) # as in ?SSlogis
Instead of calling the SSlogis, you could modify the above statement to suit your needs. I believe you would wish to see if the gender has effect on a fixed effect. Here is example code for modifying a gender specific Asym subpopulation effect in Asym2:
# Just for loading the data, we will use lme4 for model fitting, not nlme
library(nlme)
library(lme4)
# Careful when loading both nlme and lme4 as they have overlap, strange behaviour may occur
# A more generalized form could be taken e.g. from http://en.wikipedia.org/wiki/Generalised_logistic_curve
# A custom model structure:
Model <- function(age, Asym, Asym2, xmid, scal, Gender)
{
# Taken from ?SSlogis, standard form:
#Asym/(1+exp((xmid-input)/scal))
# Add gender-specific term to Asym2
(Asym+Asym2*Gender)/(1+exp((xmid-age)/scal))
# Evaluation of above form is returned by this function
}
# Model gradient, notice that we include all
# estimated fixed effects like 'Asym', 'Asym2', 'xmid' and 'scal' here,
# but not covariates from the data: 'age' and 'Gender'
ModelGradient <- deriv(
body(Model)[[2]],
namevec = c("Asym", "Asym2", "xmid", "scal"),
function.arg=Model
)
A rather typical way of introducing a gender effect is with binary coding. I will transform the Sex-variable to a binary coded Gender:
# Binary coding for the gender
Orthodont2 <- data.frame(Orthodont, Gender = as.numeric(Orthodont[,"Sex"])-1)
#> table(Orthodont2[,"Gender"])
# 0 1
#64 44
# Ordering data based on factor levels so they don't mix up paneling in lattice later on
Orthodont2 <- Orthodont2[order(Orthodont2[,"Subject"]),]
I can then fit the customized model:
# Fit the non-linear mixed effects model
fit <- nlmer(
# Response
distance ~
# Fixed effects
ModelGradient(age = age, Asym, Asym2, xmid, scal, Gender = Gender) ~
# replaces: SSlogis(age,Asym, xmid, scal) ~
# Random effects
(Asym | Subject) + (xmid | Subject),
# Data
data = Orthodont2,
start = c(Asym = 25, Asym2 = 15, xmid = 11, scal = 3))
What happens is that when Gender==0 (Male), the model achieves values:
(Asym+Asym2*0)/(1+exp((xmid-age)/scal)) = (Asym)/(1+exp((xmid-age)/scal))
which is actually the standard SSlogis-function form. However, there is now the binary switch that if Gender==1 (Female):
(Asym+Asym2)/(1+exp((xmid-age)/scal))
so that the asymptotic level that we achieve as age increases is actually Asym + Asym2, not just Asym, for female individuals.
Notice also that I do not specify a new random effect for Asym2. Because Asym is non-specific to the gender, female individuals can also have variance in their individuals asymptotic levels due to Asym-term. Model fit:
> summary(fit)
Nonlinear mixed model fit by the Laplace approximation
Formula: distance ~ ModelGradient(age = age, Asym, Asym2, xmid, scal, Gender = Gender) ~ (Asym | Subject) + (xmid | Subject)
Data: Orthodont2
AIC BIC logLik deviance
268.7 287.5 -127.4 254.7
Random effects:
Groups Name Variance Std.Dev.
Subject Asym 7.0499 2.6552
Subject xmid 4.4285 2.1044
Residual 1.5354 1.2391
Number of obs: 108, groups: Subject, 27
Fixed effects:
Estimate Std. Error t value
Asym 29.882 1.947 15.350
Asym2 -3.493 1.222 -2.859
xmid 1.240 1.068 1.161
scal 5.532 1.782 3.104
Correlation of Fixed Effects:
Asym Asym2 xmid
Asym2 -0.471
xmid -0.584 0.167
scal 0.901 -0.239 -0.773
Looks like there might be a gender specific effect (t -2.859), so that female patients seem to reach a bit lower values of 'distance' as 'age' increases: 29.882 - 3.493 = 26.389
I'm not necessarily suggesting that this is a good/best model, just showing how you could go on with customizing the non-linear models in lme4. Visualizations for the model require a bit of tinkering if you want to extract the non-linear fixed effects (in similar fashion to the visualization for linear models in How do I extract lmer fixed effects by observation? ):
# Extracting fixed effects components by calling the model function, a bit messy but it works
# I like to do this for visualizing the model fit
fixefmat <- matrix(rep(fixef(fit), times=dim(Orthodont2)[1]), ncol=length(fixef(fit)), byrow=TRUE)
colnames(fixefmat) <- names(fixef(fit))
Orthtemp <- data.frame(fixefmat, Orthodont2)
attach(Orthtemp)
# see str(Orthtemp)
# Evaluate the function for rows of the attached data.frame to extract fixed effects corresponding to observations
fix = as.vector(as.formula(body(Model)[[2]]))
detach(Orthtemp)
nobs <- 4 # 4 observations per subject
legend = list(text=list(c("y", "Xb + Zu", "Xb")), lines = list(col=c("blue", "red", "black"), pch=c(1,1,1), lwd=c(1,1,1), type=c("b","b","b")))
require(lattice)
xyplot(
distance ~ age | Subject,
data = Orthodont2,
panel = function(x, y, ...){
panel.points(x, y, type='b', col='blue')
panel.points(x, fix[(1+nobs*(panel.number()-1)):(nobs*(panel.number()))], type='b', col='black')
panel.points(x, fitted(fit)[(1+nobs*(panel.number()-1)):(nobs*(panel.number()))], type='b', col='red')
},
key = legend
)
# Residuals
plot(Orthodont2[,"distance"], resid(fit), xlab="y", ylab="e")
# Distribution of random effects
par(mfrow=c(1,2))
hist(ranef(fit)[[1]][,1], xlab="Random 'Asym'", main="")
hist(ranef(fit)[[1]][,2], xlab="Random 'xmid'", main="")
# Random 'xmid' seems a bit skewed to the right and may violate normal distribution assumption
# This is due to M13 having a bit abnormal growth curve (random effects):
# Asym xmid
#M13 3.07301310 3.9077583
Graphics output:
Notice how in above figure the Female (F##) individuals are slightly lower than their Male (M##) counterparts (black lines). E.g. M10 <-> F10 difference in the middle area panels.
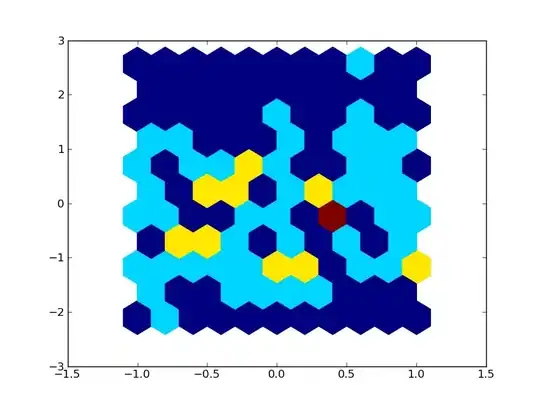
Residuals and random effects for observing some characteristics of the specified model. Individual M13 seems a bit tricky.
Using the lme4 package I can fit a nonlinear mixed effects model using a logistic curve as my functional form. I can choose to have the asymptote and midpoint entered as random effects
