Kth smallest element in sorted matrix

Question

This is an interview question.

Find the K^th smallest element in a matrix with sorted rows and columns.
Is it correct that the K^th smallest element is one of a[i, j] such as i + j = K ?

Answer 1

False.

Consider a simple matrix like this one:

1 3 5
2 4 6
7 8 9

9 is the largest (9th smallest) element. But 9 is at A[3, 3], and 3+3 != 9. (No matter what indexing convention you use, it cannot be true).

---

You can solve this problem in O(k log n) time by merging the rows incrementally, augmented with a heap to efficiently find the minimum element.

Basically, you put the elements of the first column into a heap and track the row they came from. At each step, you remove the minimum element from the heap and push the next element from the row it came from (if you reach the end of the row, then you don't push anything). Both removing the minimum and adding a new element cost O(log n). At the jth step, you remove the jth smallest element, so after k steps you are done for a total cost of O(k log n) operations (where n is the number of rows in the matrix).

For the matrix above, you initially start with 1,2,7 in the heap. You remove 1 and add 3 (since the first row is 1 3 5) to get 2,3,7. You remove 2 and add 4 to get 3,4,7. Remove 3 and add 5 to get 4,5,7. Remove 4 and add 6 to get 5,6,7. Note that we are removing the elements in the globally sorted order. You can see that continuing this process will yield the kth smallest element after k iterations.

(If the matrix has more rows than columns, then operate on the columns instead to reduce the running time.)

Answer 2

O(k log(k)) solution.

• Build a minheap.

• Add (0,0) to the heap. While, we haven't found the kth smallest element, remove the top element (x,y) from heap and add next two elements [(x+1,y) and (x,y+1)] if they haven't been visited before.

We are doing O(k) operations on a heap of size O(k) and hence the complexity.

Answer 3

This problem can be solved using binary search and optimised counting in a sorted Matrix. A binary search takes O(log(n)) time and for each search value it takes n iterations on average to find the numbers that are smaller than the searched number. The search space for binary search is limited to the minimum value in the Matrix at mat[0][0] and the maximum value mat[n-1][n-1].

For every number that is chosen from the binary search we need to count the numbers that are smaller than or equal to that particular number. And thus the 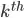smallest number can be found.

For better understanding you can refer to this video:

https://www.youtube.com/watch?v=G5wLN4UweAM&t=145s

Answer 4

Start traversing the matrix from the top-left corner (0,0) and use a binary heap for storing the "frontier" - a border between a visited part of the matrix and the rest of it.

Implementation in Java:

private static class Cell implements Comparable<Cell> {

    private final int x;
    private final int y;
    private final int value;

    public Cell(int x, int y, int value) {
        this.x = x;
        this.y = y;
        this.value = value;
    }

    @Override
    public int compareTo(Cell that) {
        return this.value - that.value;
    }

}

private static int findMin(int[][] matrix, int k) {

    int min = matrix[0][0];

    PriorityQueue<Cell> frontier = new PriorityQueue<>();
    frontier.add(new Cell(0, 0, min));

    while (k > 1) {

        Cell poll = frontier.remove();

        if (poll.y + 1 < matrix[poll.x].length) frontier.add(new Cell(poll.x, poll.y + 1, matrix[poll.x][poll.y + 1]));
        if (poll.x + 1 < matrix.length) frontier.add(new Cell(poll.x + 1, poll.y, matrix[poll.x + 1][poll.y]));

        if (poll.value > min) {
            min = poll.value;
            k--;
        }

    }

    return min;

}

Answer 5

As people mentioned previously the easiest way is to build a min heap. Here's a Java implementation using PriorityQueue:

private int kthSmallestUsingHeap(int[][] matrix, int k) {

    int n = matrix.length;

    // This is not necessary since this is the default Int comparator behavior
    Comparator<Integer> comparator = new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    };

    // building a minHeap
    PriorityQueue<Integer> pq = new PriorityQueue<>(n*n, comparator);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            pq.add(matrix[i][j]);
        }
    }

    int ans = -1;
    // remove the min element k times
    for (int i = 0; i < k; i++) {
        ans = pq.poll();
    }

    return ans;
}

Answer 6

Kth smallest element in the matrix :

The problem can be narrowed down as below.

if k is 20, then take k*k matrix (where answer will definitely lie.)

Now you can merge the rows in pair repeatedly to build a sorted array and then find the kth smallest number.

Answer 7

//int arr[][] = {{1, 5, 10, 14},
//        {2, 7, 12, 16},
//        {4, 10, 15, 20},
//        {6, 13, 19, 22}
//};
// O(k) Solution
public static int myKthElement(int arr[][], int k) {
    int lRow = 1;
    int lCol = 0;
    int rRow = 0;
    int rCol = 1;
    int count = 1;

    int row = 0;
    int col = 0;

    if (k == 1) {
        return arr[row][col];
    }

    int n = arr.length;
    if (k > n * n) {
        return -1;
    }

    while (count < k) {
        count++;

        if (arr[lRow][lCol] < arr[rRow][rCol]) {
            row = lRow;
            col = lCol;

            if (lRow < n - 1) {
                lRow++;
            } else {
                if (lCol < n - 1) {
                    lCol++;
                }

                if (rRow < n - 1) {
                    lRow = rRow + 1;
                }
            }
        } else {
            row = rRow;
            col = rCol;

            if (rCol < n - 1) {
                rCol++;
            } else {
                if (rRow < n - 1) {
                    rRow++;
                }
                if (lCol < n - 1) {
                    rCol = lCol + 1;
                }
            }
        }
    }

    return arr[row][col];
}