How is the derivative of a f(x) typically calculated programmatically to ensure maximum accuracy?
I am implementing the Newton-Raphson method, and it requires taking of the derivative of a function.
How is the derivative of a f(x) typically calculated programmatically to ensure maximum accuracy?
I am implementing the Newton-Raphson method, and it requires taking of the derivative of a function.
I agree with @erikkallen that (f(x + h) - f(x - h)) / 2 * h is the usual approach for numerically approximating derivatives. However, getting the right step size h is a little subtle.
The approximation error in (f(x + h) - f(x - h)) / 2 * h decreases as h gets smaller, which says you should take h as small as possible. But as h gets smaller, the error from floating point subtraction increases since the numerator requires subtracting nearly equal numbers. If h is too small, you can loose a lot of precision in the subtraction. So in practice you have to pick a not-too-small value of h that minimizes the combination of approximation error and numerical error.
As a rule of thumb, you can try h = SQRT(DBL_EPSILON) where DBL_EPSILON is the smallest double precision number e such that 1 + e != 1 in machine precision. DBL_EPSILON is about 10^-15 so you could use h = 10^-7 or 10^-8.
For more details, see these notes on picking the step size for differential equations.
Newton_Raphson assumes that you can have two functions f(x) and its derivative f'(x). If you do not have the derivative available as a function and have to estimate the derivative from the original function then you should use another root finding algorithm.
Wikipedia root finding gives several suggestions as would any numerical analysis text.
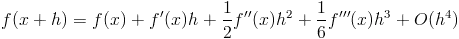
1) First case:

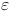 — relative rounding error, about 2^{-16} for double and 2^{-7} for float.
— relative rounding error, about 2^{-16} for double and 2^{-7} for float.
We can calculate total error:
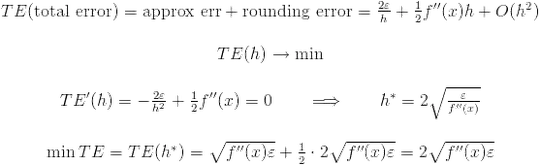
Suppose that you are using double floating operation. Thus the optimal value of h is 2sqrt(DBL_EPSILON/f''(x)). You do not know f''(x). But you have to estimate this value. For example, if f''(x) is about 1 then the optimal value of h is 2^{-7} but if f''(x) is about 10^6 then the optimal value of h is 2^{-10}!
2) Second case:

Note that second approximation error tends to 0 faster than first one. But if f'''(x) is very lagre then first option is more preferable:
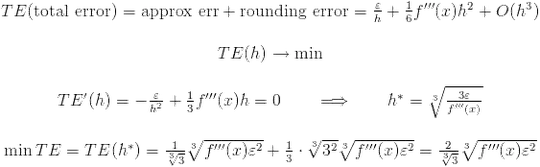
Note that in the first case h is proportional to e but in the second case h is proportional to e^{1/3}. For double floating operations e^{1/3} is 2^{-5} or 2^{-6}. (I suppose that f'''(x) is about 1).
Which way is better? It is unkown if you do not know f''(x) and f'''(x) or you can not estimate these values. It is believed that the second option is preferable. But if you know that f'''(x) is very large use first one.
What is the optimal value of h? Suppose that f''(x) and f'''(x) are about 1. Also assume that we use double floating operations. Then in the first case h is about 2^{-8}, in the first case h is about 2^{-5}. Correct this values if you know f''(x) or f'''(x).
fprime(x) = (f(x+dx) - f(x-dx)) / (2*dx)
for some small dx.
What do you know about f(x)? If you only have f as a black box the only thing you can do is to numerically approximate the derivative. But the accuracy is usually not that good.
You can do much better if you can touch the code that computes f. Try "automatic differentiation". There some nice libraries for that available. With a bit of library magic you can convert your function easily to something that computes the derivative automatically. For a simple C++ example, see the source code in this German discussion.
You definitely want to take into account John Cook's suggestion for picking h, but you typically don't want to use a centered difference to approximate the derivative. The main reason is that it costs an extra function evaluation, if you use a forward difference, ie,
f'(x) = (f(x+h) - f(x))/h
Then you'll get value of f(x) for free because you need to compute it already for Newton's method. This isn't such a big deal when you have a scalar equation, but if x is a vector, then f'(x) is a matrix (the Jacobian), and you'll need to do n extra function evaluations to approximate it using the centered difference approach.
In addition to John D. Cooks answer above it is important not only to take into account the floating point precision, but also the robustness of the function f(x). For instance, in finance, it is a common case that f(x) is actually a Monte Carlo-simulation and the value of f(x) has some noise. Using a very small step size can in these cases severely degrade the accuracy of the derivative.
Typically signal noise impacts the derivative quality more that anything else. If you do have noise in your f(x), Savtizky-Golay is a excellent smoothing algorithm that is often used to compute good derivatives. In a nutshell, SG fits a polynomial locally to your data, the then this polynomial can be used to compute the derivative.
Paul