Distance between 2 hexagons on hexagon grid

Question

I have a hexagon grid:

with template type coordinates T. How I can calculate distance between two hexagons?

For example:

dist((3,3), (5,5)) = 3

dist((1,2), (1,4)) = 2

Answer 1

First apply the transform (y, x) |-> (u, v) = (x, y + floor(x / 2)).

Now the facial adjacency looks like

 0 1 2 3
0*-*-*-*
 |\|\|\|
1*-*-*-*
 |\|\|\|
2*-*-*-*

Let the points be (u1, v1) and (u2, v2). Let du = u2 - u1 and dv = v2 - v1. The distance is

if du and dv have the same sign: max(|du|, |dv|), by using the diagonals
if du and dv have different signs: |du| + |dv|, because the diagonals are unproductive

In Python:

def dist(p1, p2):
    y1, x1 = p1
    y2, x2 = p2
    du = x2 - x1
    dv = (y2 + x2 // 2) - (y1 + x1 // 2)
    return max(abs(du), abs(dv)) if ((du >= 0 and dv >= 0) or (du < 0 and dv < 0)) else abs(du) + abs(dv)

Answer 2

Posting here after I saw a blog post of mine had gotten referral traffic from another answer here. It got voted down, rightly so, because it was incorrect; but it was a mischaracterization of the solution put forth in my post.

Your 'squiggly' axis - in terms of your x coordinate being displaced every other row - is going to cause you all sorts of headaches with trying to determine distances or doing pathfinding later on, if this is for a game of some sort. Hexagon grids lend themselves to three axes naturally, and a 'squared off' grid of hexagons will optimally have some negative coordinates, which allows for simpler math around distances.

Here's a grid with (x,y) mapped out, with x increasing to the lower right, and y increasing upwards.

By straightening things out, the third axis becomes obvious.

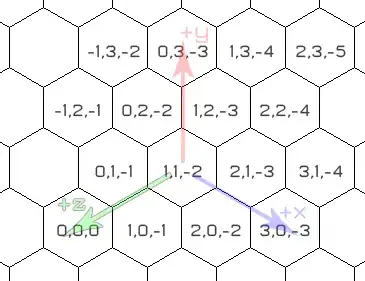
The neat thing about this, is that the three coordinates become interlinked - the sum of all three coordinates will always be 0.

With such a consistent coordinate system, the atomic distance between any two hexes is the largest change between the three coordinates, or:

d = max( abs(x1 - x2), abs(y1 -y2), abs( (-x1 + -y1) - (-x2 + -y2) )

Pretty straightforward. But you must fix your grid first!

Answer 3

The correct explicit formula for the distance, with your coordinate system, is given by:

d((x1,y1),(x2,y2)) = max( abs(x1 - x2), 
                          abs((y1 + floor(x1/2)) - (y2 + floor(x2/2)))
                        )

Answer 4

Here is what a did:

Taking one cell as center (it is easy to see if you choose 0,0), cells at distance dY form a big hexagon (with “radius” dY). One vertices of this hexagon is (dY2,dY). If dX<=dY2 the path is a zig-zag to the ram of the big hexagon with a distance dY. If not, then the path is the “diagonal” to the vertices, plus an vertical path from the vertices to the second cell, with add dX-dY2 cells.

Maybe better to understand: led:

dX = abs(x1 - x2);
dY = abs(y1 - y2);
dY2= floor((abs(y1 - y2) +  (y1+1)%2  ) / 2);

Then:

 d = d((x1,y1),(x2,y2)) 
   = dX < dY2 ? dY : dY + dX-dY2 + y1%2 * dY%2

Answer 5

First, you need to transform your coordinates to a "mathematical" coordinate system. Every two columns you shift your coordinates by 1 unit in the y-direction. The "mathamatical" coordinates (s, t) can be calculated from your coordinates (u,v) as follows:

s = u + floor(v/2) t = v

If you call one side of your hexagons a, the basis vectors of your coordinate system are (0, -sqrt(3)a) and (3a/2, sqrt(3)a/2). To find the minimum distance between your points, you need to calculate the manhattan distance in your coordinate system, which is given by |s1-s2|+|t1-t2| where s and t are the coordinates in your system. The manhattan distance only covers walking in the direction of your basis vectors so it only covers walking like that: |/ but not walking like that: |\. You need to transform your vectors into another coordinate system with basis vectors (0, -sqrt(3)a) and (3a/2, -sqrt(3)a/2). The coordinates in this system are given by s'=s-t and t'=t so the manhattan distance in this coordinate system is given by |s1'-s2'|+|t1'-t2'|. The distance you are looking for is the minimum of the two calculated manhattan distances. Your code would look like this:

struct point
{
  int u;
  int v;
}

int dist(point const & p, point const & q)
{
  int const ps = p.u + (p.v / 2); // integer division!
  int const pt = p.v;
  int const qs = q.u + (q.v / 2);
  int const qt = q.v;
  int const dist1 = abs(ps - qs) + abs(pt - qt);
  int const dist2 = abs((ps - pt) - (qs - qt)) + abs(pt - qt);
  return std::min(dist1, dist2);
}

Answer 6

(odd-r)(without z, only x,y)

I saw some problems with realizations above. Sorry, I didn't check it all but. But maybe my solution will be helpful for someone and maybe it's a bad and not optimized solution.

The main idea to go by diagonal and then by horizontal. But for that we need to note:

1) For example, we have 0;3 (x1=0;y1=3) and to go to the y2=6 we can handle within 6 steps to each point (0-6;6) so: 0-left_border , 6-right_border

2)Calculate some offsets

#include <iostream>
#include <cmath>

int main()
{
    //while(true){
    int x1,y1,x2,y2;
    std::cin>>x1>>y1;
    std::cin>>x2>>y2;
    int diff_y=y2-y1; //only up-> bottom no need abs
    int left_x,right_x;
    int path;

    if( y1>y2 ) { // if Down->Up  then swap
        int temp_y=y1;
        y1=y2;
        y2=temp_y;
        //
        int temp_x=x1;
        x1=x2;
        x2=temp_x;
    }                   // so now we have Up->Down

        // Note that it's odd-r horizontal layout
        //OF - Offset Line  (y%2==1)
        //NOF -Not Offset Line (y%2==0)
    if( y1%2==1 && y2%2==0 ){ //OF ->NOF
        left_x = x1 - ( (y2 - y1 + 1)/2 -1 );  //UP->DOWN no need abs
        right_x = x1 + (y2 - y1 + 1)/2;  //UP->DOWN no need abs
    }
    else if( y1%2==0 && y2%2==1 ){ // OF->NOF
        left_x = x1 - (y2 - y1 + 1)/2;  //UP->DOWN no need abs
        right_x = x1 + ( (y2 - y1 + 1)/2 -1 );  //UP->DOWN no need abs

    }
    else{
        left_x = x1 - (y2 - y1 + 1)/2;  //UP->DOWN no need abs
        right_x = x1 + (y2 - y1 + 1)/2;  //UP->DOWN no need abs
    }
    /////////////////////////////////////////////////////////////
    if( x2>=left_x && x2<=right_x ){
        path = y2 - y1;
    }
    else {
        int min_1 = std::abs( left_x - x2 );
        int min_2 = std::abs( right_x - x2 );
        path = y2 - y1 + std::min(min_1, min_2);
    }
    std::cout<<"Path: "<<path<<"\n\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\n";
    //}

    return 0;
}

Answer 7

I believe the answer you seek is:

d((x1,y1),(x2,y2))=max(abs(x1-x2),abs(y1-y2));

You can find a good explanation on hexagonal grid coordinate-system/distances here:

http://keekerdc.com/2011/03/hexagon-grids-coordinate-systems-and-distance-calculations/