When the first row is 1, 1/2 , 1/3 ....
Here's an image to support the question.
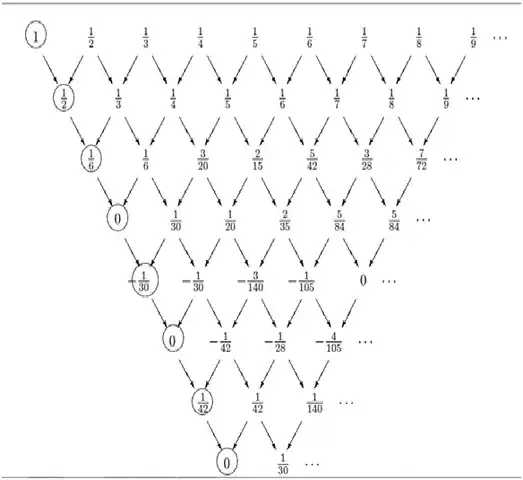
Does there exist a more efficient approach than the naive O(n^2) approach?
I came across this when studying Bernoulli numbers and then consequently on reaching "Akiyama–Tanigawa algorithm".
One of the ways could be simple precomputing the results and storing them in a table. Since Bernoulli numbers grow very quickly, for most practical purposes we wouldn't need Bernoulli numbers for much larger n. Consider Bernoulli(400)- its around -(10^550).
But looking at it only algorithmically, is there a better approach than the O(n^2) one?