I was looking for a way to do a BITOR() with an Oracle database and came across a suggestion to just use BITAND() instead, replacing BITOR(a,b) with a + b - BITAND(a,b).
I tested it by hand a few times and verified it seems to work for all binary numbers I could think of, but I can't think out quick mathematical proof of why this is correct.
Could somebody enlighten me?
A & B is the set of bits that are on in both A and B. A - (A & B) leaves you with all those bits that are only on in A. Add B to that, and you get all the bits that are on in A or those that are on in B.
Simple addition of A and B won't work because of carrying where both have a 1 bit. By removing the bits common to A and B first, we know that (A-(A&B)) will have no bits in common with B, so adding them together is guaranteed not to produce a carry.
Imagine you have two binary numbers: a and b. And let's say that these number never have 1 in the same bit at the same time, i.e. if a has 1 in some bit, the b always has 0 in the corresponding bit. And in other direction, if b has 1 in some bit, then a always has 0 in that bit. For example
a = 00100011
b = 11000100
This would be an example of a and b satisfying the above condition. In this case it is easy to see that a | b would be exactly the same as a + b.
a | b = 11100111
a + b = 11100111
Let's now take two numbers that violate our condition, i.e. two numbers have at least one 1 in some common bit
a = 00100111
b = 11000100
Is a | b the same as a + b in this case? No
a | b = 11100111
a + b = 11101011
Why are they different? They are different because when we + the bit that has 1 in both numbers, we produce so called carry: the resultant bit is 0, and 1 is carried to the next bit to the left: 1 + 1 = 10. Operation | has no carry, so 1 | 1 is again just 1.
This means that the difference between a | b and a + b occurs when and only when the numbers have at least one 1 in common bit. When we sum two numbers with 1 in common bits, these common bits get added "twice" and produce a carry, which ruins the similarity between a | b and a + b.
Now look at a & b. What does a & b calculate? a & b produces the number that has 1 in all bits where both a and b have 1. In our latest example
a = 00100111
b = 11000100
a & b = 00000100
As you saw above, these are exactly the bits that make a + b differ from a | b. The 1 in a & b indicate all positions where carry will occur.
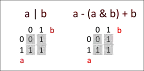
Now, when we do a - (a & b) we effectively remove (subtract) all "offending" bits from a and only such bits
a - (a & b) = 00100011
Numbers a - (a & b) and b have no common 1 bits, which means that if we add a - (a & b) and b we won't run into a carry, and, if you think about it, we should end up with the same result as if we just did a | b
a - (a & b) + b = 11100111
A&B = C where any bits left set in C are those set in both A and in B.
Either A-C = D or B-C = E sets just these common bits to 0. There is no carrying effect because 1-1=0.
D+B or E+A is similar to A+B except that because we subtracted A&B previously there will be no carry due to having cleared all commonly set bits in D or E.
The net result is that A-A&B+B or B-A&B+A is equivalent to A|B.
Here's a truth table if it's still confusing:
A | B | OR A | B | & A | B | - A | B | + ---+---+---- ---+---+--- ---+---+--- ---+---+--- 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 1 | 1 0 | 1 | 0 0 | 1 | 0-1 0 | 1 | 1 1 | 0 | 1 1 | 0 | 0 1 | 0 | 1 1 | 0 | 1 1 | 1 | 1 1 | 1 | 1 1 | 1 | 0 1 | 1 | 1+1
Notice the carry rows in the + and - operations, we avoid those because A-(A&B) sets cases were both bits in A and B are 1 to 0 in A, then adding them back from B also brings in the other cases were there was a 1 in either A or B but not where both had 0, so the OR truth table and the A-(A&B)+B truth table are identical.
Another way to eyeball it is to see that A+B is almost like A|B except for the carry in the bottom row. A&B isolates that bottom row for us, A-A&B moves those isolated cased up two rows in the + table, and the (A-A&B)+B becomes equivalent to A|B.
While you could commute this to A+B-(A&B), I was afraid of a possible overflow but that was unjustified it seems:
#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a, b, a|b, a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }
c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000
Edit: So I wrote this before there were answers, then there was some 2 hours of down time on my home connection, and I finally managed to post it, noticing only afterwards that it'd been properly answered twice. Personally I prefer referring to a truth table to work out bitwise operations, so I'll leave it in case it helps someone.
