0

In the following screen shot:

enter image description here

when you drag the tail of the word balloon (the thing that connects from the balloon to the persons mouth), the shape curves (as illustrated by the difference between the two balloon tails in the picture). I'm wondering, how is this done? I'm assuming you need to start with a CGPath and do something to it, does anyone happen to know what this is?

Update: So if I wanted to curve the following shape:

enter image description here

Would I use the following code:

CGPathAddCurveToPoint(mutablePath, NULL, x1, y1, x2, y2 + constant, x5, y5);
CGPathAddCurveToPoint(mutablePath, NULL, x3, y3, x4, y4 + constant, x5, y5);

Where the constant readjusts the y position of point 2 and point 4 to make the curve?

Ser Pounce
  • 14,196
  • 18
  • 84
  • 169

2 Answers2

6

You need to exploit the fact that, mathematically, a straight-line segment is just a kind of curve segment.

(It's easier than it sounds, trust me.)

Bézier path segments have something called “order” that essentially determines how many points there are in the segment, not counting the point you're coming from.

  • A straight-line segment is a first-order curve, meaning that it only has the destination point. These “curves” are always straight lines because there are no control points to curve toward.
  • Quadratic curves are second-order curves (one control point plus the destination).
  • Cubic curves are third-order curves (two control points).
  • (The math doesn't put any limit on this, but Quartz stops here. No fourth-order curves for you without rolling your own rasterizer.)

This matters because any lower-order curve—including a straight line—can be expressed as a higher-order curve.

So, the secret?

For even a straight tail, use a curve.

(Namely, a cubic curve, since you want the curve going in two different directions: One, more or less into the tail, and the other, more or less along the edge of the balloon.)

From each of the two points at the base of the tail, you want one of the control points to be about halfway to the destination. This much is unconditional.

The direction of each of the control points gives you three options:

The straight-out tail

Picture of a tail straight down, with the tip of the tail horizontally between the two base points, and the control points exactly halfway between each base point and the tip point.

Notice the two control points along the blue line at the vertical center of the image.

Notice the direction of these two control points, relative to the base point it's connected to. They are angled inward, toward the tip—indeed, exactly on the straight line to the tip.

The oblique tail

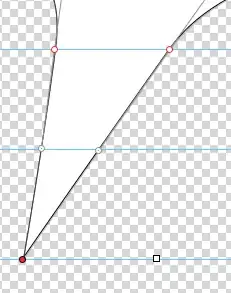
Picture of a tail that is slanted, but not curved.

Here, the tip point is no longer horizontally between the two base points. The control points have moved, but only to follow: each one is still halfway along the straight line between the corresponding base point and the tip.

The curved tail

Picture of a tail that is curved.

For a curved tail, you move the tip, but you keep the control points at the same position as for a straight tail. Thus, the tail starts out straight out (following the control points), but as it gets farther from the base points, their influence wanes, and the tail begins curving toward the tip.

This is a lot easier to describe visually than to put into code, so you may want to consider using something like PaintCode or Opacity to draw each kind of tail using a pen tool and then see what the code they generate for it looks like.

Peter Hosey
  • 95,783
  • 15
  • 211
  • 370
  • Appreciate your explanation, but I'm having a little difficulty putting it into code. Possible you could take a look at the update I've provided in the above question? – Ser Pounce Jul 11 '14 at 01:33
  • @CoDEFRo: You don't want to end on the same point in both curveto segments. The first curve arrives at point five; the second curve must *depart* from point five and end up somewhere else (point three, by your numbering). (Accordingly, you should plot to points three and four the other way round.) Here's a Gist that demonstrates my answer: https://gist.github.com/6fe77dc16c850f1630d7 Output (yours on the top, mine on the bottom): http://i.stack.imgur.com/qHkoR.png – Peter Hosey Jul 14 '14 at 14:11
  • Thank you so much for taking the time to do that, it's very helpful :) – Ser Pounce Jul 17 '14 at 13:50
  • @PeterHosey - I think there might be a more simple way to do this as evident by: http://stackoverflow.com/questions/25776819/how-to-curve-cgmutablepath (how the bubbles are also curved). – Ser Pounce Oct 22 '14 at 21:32
  • @StackOverFlowRider: I wouldn't call that “more simple” (maybe more general), but it sure is damned impressive. – Peter Hosey Oct 26 '14 at 01:04
2

You can use the CGContextAddCurveToPoint() functions:

CGContextMoveToPoint(ctx, x, y);
CGContextAddCurveToPoint(ctx, outTangentX, outTangentY, inTangentX, inTangentY, newX, newY);
... // more points or whatever you need here
CGContextFillPath(ctx); // Fill with white
CGContextStrokePath(ctx); // stroke the edges with black

The in/out tangents can be hardcoded to be something that looks good based on the point on the mouth of the picture and the point where it meets the balloon bubble. You might try something like making their angles half-way between perpendicular and the slope of the straight line between the 2 points or something like that as a starting place.

user1118321
  • 25,567
  • 4
  • 55
  • 86