Peak detection in a noisy 2d array

Question

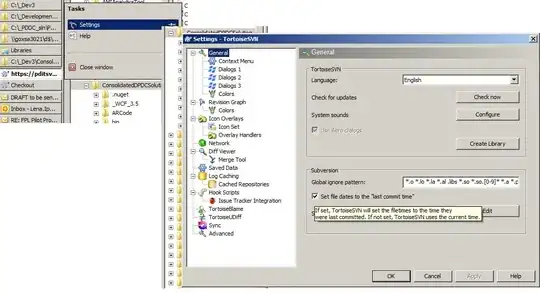
I'm trying to get python to return, as close as possible, the center of the most obvious clustering in an image like the one below:

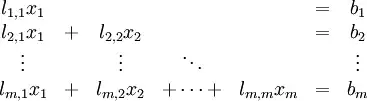
In my previous question I asked how to get the global maximum and the local maximums of a 2d array, and the answers given worked perfectly. The issue is that the center estimation I can get by averaging the global maximum obtained with different bin sizes is always slightly off than the one I would set by eye, because I'm only accounting for the biggest bin instead of a group of biggest bins (like one does by eye).

I tried adapting the answer to this question to my problem, but it turns out my image is too noisy for that algorithm to work. Here's my code implementing that answer:

import numpy as np
from scipy.ndimage.filters import maximum_filter
from scipy.ndimage.morphology import generate_binary_structure, binary_erosion
import matplotlib.pyplot as pp

from os import getcwd
from os.path import join, realpath, dirname

# Save path to dir where this code exists.
mypath = realpath(join(getcwd(), dirname(__file__)))
myfile = 'data_file.dat'

x, y = np.loadtxt(join(mypath,myfile), usecols=(1, 2), unpack=True)
xmin, xmax = min(x), max(x)
ymin, ymax = min(y), max(y)

rang = [[xmin, xmax], [ymin, ymax]]
paws = []

for d_b in range(25, 110, 25):
    # Number of bins in x,y given the bin width 'd_b'
    binsxy = [int((xmax - xmin) / d_b), int((ymax - ymin) / d_b)]

    H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
    paws.append(H)


def detect_peaks(image):
    """
    Takes an image and detect the peaks usingthe local maximum filter.
    Returns a boolean mask of the peaks (i.e. 1 when
    the pixel's value is the neighborhood maximum, 0 otherwise)
    """

    # define an 8-connected neighborhood
    neighborhood = generate_binary_structure(2,2)

    #apply the local maximum filter; all pixel of maximal value 
    #in their neighborhood are set to 1
    local_max = maximum_filter(image, footprint=neighborhood)==image
    #local_max is a mask that contains the peaks we are 
    #looking for, but also the background.
    #In order to isolate the peaks we must remove the background from the mask.

    #we create the mask of the background
    background = (image==0)

    #a little technicality: we must erode the background in order to 
    #successfully subtract it form local_max, otherwise a line will 
    #appear along the background border (artifact of the local maximum filter)
    eroded_background = binary_erosion(background, structure=neighborhood, border_value=1)

    #we obtain the final mask, containing only peaks, 
    #by removing the background from the local_max mask
    detected_peaks = local_max - eroded_background

    return detected_peaks


#applying the detection and plotting results
for i, paw in enumerate(paws):
    detected_peaks = detect_peaks(paw)
    pp.subplot(4,2,(2*i+1))
    pp.imshow(paw)
    pp.subplot(4,2,(2*i+2) )
    pp.imshow(detected_peaks)

pp.show()

and here's the result of that (varying the bin size):

enter image description here

Clearly my background is too noisy for that algorithm to work, so the question is: how can I make that algorithm less sensitive? If an alternative solution exists then please let me know.

EDIT

Following Bi Rico advise I attempted smoothing my 2d array before passing it on to the local maximum finder, like so:

H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
H1 = gaussian_filter(H, 2, mode='nearest')
paws.append(H1)

These were the results with a sigma of 2, 4 and 8:

enter image description here

EDIT 2

A mode ='constant' seems to work much better than nearest. It converges to the right center with a sigma=2 for the largest bin size:

enter image description here

So, how do I get the coordinates of the maximum that shows in the last image?

Have you tried smoothing your data before applying your algorithm? A Gaussian and/or median filters might help. — Bi Rico, May 30 '13 at 18:20
How well can you describe the properties of the peak(s) you are trying to detect? Is it always a single peak? Do you expect it to be symmetric, or to have a characteristic spatial scale? Also, what are the properties of the background noise - is it spatially structured? — ali_m, Jun 14 '13 at 22:28
The answers to those questions are: I can hardly describe them since they are very variable, it is not always a single peak, the peaks are not symmetric and have no particular spatial scale and the background noise is pretty much random (ie: it can be smooth and very dense, it can be clumped and hard to distinguish from a real "peak" and it can be very weak) I am aware this sounds like an issue too broad to be resolved in an _one size fits all_ algorithmic approach which is why I have little hope in finding a somewhat simple answer. — Gabriel, Jun 15 '13 at 03:22

Alejandro · Answer 1 · 2016-04-10T14:15:02.860

Answering the last part of your question, always you have points in an image, you can find their coordinates by searching, in some order, the local maximums of the image. In case your data is not a point source, you can apply a mask to each peak in order to avoid the peak neighborhood from being a maximum while performing a future search. I propose the following code:

import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
import copy

def get_std(image):
    return np.std(image)

def get_max(image,sigma,alpha=20,size=10):
    i_out = []
    j_out = []
    image_temp = copy.deepcopy(image)
    while True:
        k = np.argmax(image_temp)
        j,i = np.unravel_index(k, image_temp.shape)
        if(image_temp[j,i] >= alpha*sigma):
            i_out.append(i)
            j_out.append(j)
            x = np.arange(i-size, i+size)
            y = np.arange(j-size, j+size)
            xv,yv = np.meshgrid(x,y)
            image_temp[yv.clip(0,image_temp.shape[0]-1),
                                   xv.clip(0,image_temp.shape[1]-1) ] = 0
            print xv
        else:
            break
    return i_out,j_out

#reading the image   
image = mpimg.imread('ggd4.jpg')
#computing the standard deviation of the image
sigma = get_std(image)
#getting the peaks
i,j = get_max(image[:,:,0],sigma, alpha=10, size=10)

#let's see the results
plt.imshow(image, origin='lower')
plt.plot(i,j,'ro', markersize=10, alpha=0.5)
plt.show()

The image ggd4 for the test can be downloaded from:

http://www.ipac.caltech.edu/2mass/gallery/spr99/ggd4.jpg

The first part is to get some information about the noise in the image. I did it by computing the standard deviation of the full image (actually is better to select an small rectangle without signal). This is telling us how much noise is present in the image. The idea to get the peaks is to ask for successive maximums, which are above of certain threshold (let's say, 3, 4, 5, 10, or 20 times the noise). This is what the function get_max is actually doing. It performs the search of maximums until one of them is below the threshold imposed by the noise. In order to avoid finding the same maximum many times it is necessary to remove the peaks from the image. In the general way, the shape of the mask to do so depends strongly on the problem that one want to solve. for the case of stars, it should be good to remove the star by using a Gaussian function, or something similar. I have chosen for simplicity a square function, and the size of the function (in pixels) is the variable "size". I think that from this example, anybody can improve the code by adding more general things.

EDIT:

The original image looks like:

While the image after identifying the luminous points looks like this:

msarahan · Answer 2 · 2013-08-04T05:18:52.913

Too much of a n00b on Stack Overflow to comment on Alejandro's answer elsewhere here. I would refine his code a bit to use a preallocated numpy array for output:

def get_max(image,sigma,alpha=3,size=10):
    from copy import deepcopy
    import numpy as np
    # preallocate a lot of peak storage
    k_arr = np.zeros((10000,2))
    image_temp = deepcopy(image)
    peak_ct=0
    while True:
        k = np.argmax(image_temp)
        j,i = np.unravel_index(k, image_temp.shape)
        if(image_temp[j,i] >= alpha*sigma):
            k_arr[peak_ct]=[j,i]
            # this is the part that masks already-found peaks.
            x = np.arange(i-size, i+size)
            y = np.arange(j-size, j+size)
            xv,yv = np.meshgrid(x,y)
            # the clip here handles edge cases where the peak is near the 
            #    image edge
            image_temp[yv.clip(0,image_temp.shape[0]-1),
                               xv.clip(0,image_temp.shape[1]-1) ] = 0
            peak_ct+=1
        else:
            break
    # trim the output for only what we've actually found
    return k_arr[:peak_ct]

In profiling this and Alejandro's code using his example image, this code about 33% faster (0.03 sec for Alejandro's code, 0.02 sec for mine.) I expect on images with larger numbers of peaks, it would be even faster - appending the output to a list will get slower and slower for more peaks.

score 3 · Answer 3 · answered Jul 03 '13 at 22:12

I think the first step needed here is to express the values in H in terms of the standard deviation of the field:

import numpy as np
H = H / np.std(H)

Now you can put a threshold on the values of this H. If the noise is assumed to be Gaussian, picking a threshold of 3 you can be quite sure (99.7%) that this pixel can be associated with a real peak and not noise. See here.

Now the further selection can start. It is not exactly clear to me what exactly you want to find. Do you want the exact location of peak values? Or do you want one location for a cluster of peaks which is in the middle of this cluster?
Anyway, starting from this point with all pixel values expressed in standard deviations of the field, you should be able to get what you want. If you want to find clusters you could perform a nearest neighbour search on the >3-sigma gridpoints and put a threshold on the distance. I.e. only connect them when they are close enough to each other. If several gridpoints are connected you can define this as a group/cluster and calculate some (sigma-weighted?) center of the cluster. Hope my first contribution on Stackoverflow is useful for you!

score 2 · Answer 4 · answered May 30 '13 at 21:19

The way I would do it:

1) normalize H between 0 and 1.

2) pick a threshold value, as tcaswell suggests. It could be between .9 and .99 for example

3) use masked arrays to keep only the x,y coordinates with H above threshold:

import numpy.ma as ma
x_masked=ma.masked_array(x, mask= H < thresold)
y_masked=ma.masked_array(y, mask= H < thresold)

4) now you can weight-average on the masked coordinates, with weight something like (H-threshold)^2, or any other power greater or equal to one, depending on your taste/tests.

Comment: 1) This is not robust with respect to the type of peaks you have, since you may have to adapt the thresold. This is the minor problem; 2) This DOES NOT work with two peaks as it is, and will give wrong results if the 2nd peak is above threshold.

Nonetheless, it will always give you an answer without crashing (with pros and cons of the thing..)

score 2 · Accepted Answer · edited May 23 '17 at 12:16

I'm adding this answer because it's the solution I ended up using. It's a combination of Bi Rico's comment here (May 30 at 18:54) and the answer given in this question: Find peak of 2d histogram.

As it turns out using the peak detection algorithm from this question Peak detection in a 2D array only complicates matters. After applying the Gaussian filter to the image all that needs to be done is to ask for the maximum bin (as Bi Rico pointed out) and then obtain the maximum in coordinates.

So instead of using the detect-peaks function as I did above, I simply add the following code after the Gaussian 2D histogram is obtained:

# Get 2D histogram.
H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
# Get Gaussian filtered 2D histogram.
H1 = gaussian_filter(H, 2, mode='nearest')
# Get center of maximum in bin coordinates.
x_cent_bin, y_cent_bin = np.unravel_index(H1.argmax(), H1.shape)
# Get center in x,y coordinates.
x_cent_coor , y_cent_coord = np.average(xedges[x_cent_bin:x_cent_bin + 2]), np.average(yedges[y_cent_g:y_cent_g + 2])

Peak detection in a noisy 2d array

EDIT

EDIT 2

5 Answers5