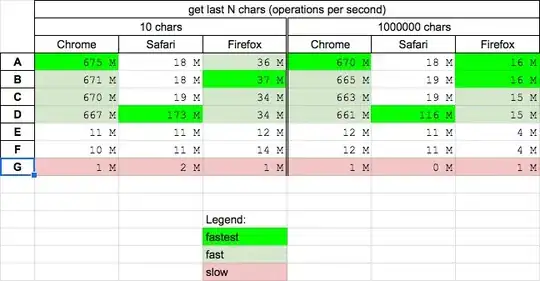
This is a basic transform question in PIL. I've tried at least a couple of times in the past few years to implement this correctly and it seems there is something I don't quite get about Image.transform in PIL. I want to implement a similarity transformation (or an affine transformation) where I can clearly state the limits of the image. To make sure my approach works I implemented it in Matlab.
The Matlab implementation is the following:
im = imread('test.jpg');
y = size(im,1);
x = size(im,2);
angle = 45*3.14/180.0;
xextremes = [rot_x(angle,0,0),rot_x(angle,0,y-1),rot_x(angle,x-1,0),rot_x(angle,x-1,y-1)];
yextremes = [rot_y(angle,0,0),rot_y(angle,0,y-1),rot_y(angle,x-1,0),rot_y(angle,x-1,y-1)];
m = [cos(angle) sin(angle) -min(xextremes); -sin(angle) cos(angle) -min(yextremes); 0 0 1];
tform = maketform('affine',m')
round( [max(xextremes)-min(xextremes), max(yextremes)-min(yextremes)])
im = imtransform(im,tform,'bilinear','Size',round([max(xextremes)-min(xextremes), max(yextremes)-min(yextremes)]));
imwrite(im,'output.jpg');
function y = rot_x(angle,ptx,pty),
y = cos(angle)*ptx + sin(angle)*pty
function y = rot_y(angle,ptx,pty),
y = -sin(angle)*ptx + cos(angle)*pty
this works as expected. This is the input:
and this is the output:

This is the Python/PIL code that implements the same transformation:
import Image
import math
def rot_x(angle,ptx,pty):
return math.cos(angle)*ptx + math.sin(angle)*pty
def rot_y(angle,ptx,pty):
return -math.sin(angle)*ptx + math.cos(angle)*pty
angle = math.radians(45)
im = Image.open('test.jpg')
(x,y) = im.size
xextremes = [rot_x(angle,0,0),rot_x(angle,0,y-1),rot_x(angle,x-1,0),rot_x(angle,x-1,y-1)]
yextremes = [rot_y(angle,0,0),rot_y(angle,0,y-1),rot_y(angle,x-1,0),rot_y(angle,x-1,y-1)]
mnx = min(xextremes)
mxx = max(xextremes)
mny = min(yextremes)
mxy = max(yextremes)
im = im.transform((int(round(mxx-mnx)),int(round((mxy-mny)))),Image.AFFINE,(math.cos(angle),math.sin(angle),-mnx,-math.sin(angle),math.cos(angle),-mny),resample=Image.BILINEAR)
im.save('outputpython.jpg')
and this is the output from Python:
I've tried this with several versions of Python and PIL on multiple OSs through the years and the results is always mostly the same.
This is the simplest possible case that illustrates the problem, I understand that if it was a rotation I wanted, I could do the rotation with the im.rotate call but I want to shear and scale too, this is just an example to illustrate a problem. I would like to get the same output for all affine transformations. I would like to be able to get this right.
EDIT:
If I change the transform line to this:
im = im.transform((int(round(mxx-mnx)),int(round((mxy-mny)))),Image.AFFINE,(math.cos(angle),math.sin(angle),0,-math.sin(angle),math.cos(angle),0),resample=Image.BILINEAR)
this is the output I get:
EDIT #2
I rotated by -45 degrees and changed the offset to -0.5*mnx and -0.5*mny and obtained this:

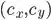 of the image, and translate the image by
of the image, and translate the image by 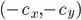 , so the center of the image is at the origin
, so the center of the image is at the origin 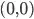 .
.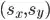 .
.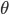 .
.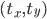 of the image, and translate the image by
of the image, and translate the image by 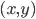 :
: 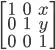
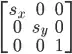
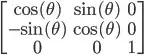
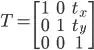

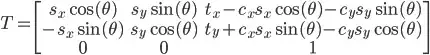
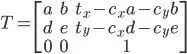
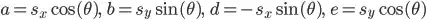 .
.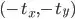
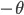 .
.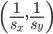 .
.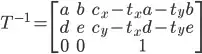
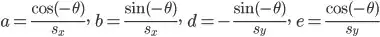 .
.