How to get an average picture from 100 pictures using PIL?

Question

For example, I have 100 pictures whose resolution is the same, and I want to merge them into one picture. For the final picture, the RGB value of each pixel is the average of the 100 pictures' at that position. I know the getdata function can work in this situation, but is there a simpler and faster way to do this in PIL(Python Image Library)?

Answer 1

Let's assume that your images are all .png files and they are all stored in the current working directory. The python code below will do what you want. As Ignacio suggests, using numpy along with PIL is the key here. You just need to be a little bit careful about switching between integer and float arrays when building your average pixel intensities.

import os, numpy, PIL
from PIL import Image

# Access all PNG files in directory
allfiles=os.listdir(os.getcwd())
imlist=[filename for filename in allfiles if  filename[-4:] in [".png",".PNG"]]

# Assuming all images are the same size, get dimensions of first image
w,h=Image.open(imlist[0]).size
N=len(imlist)

# Create a numpy array of floats to store the average (assume RGB images)
arr=numpy.zeros((h,w,3),numpy.float)

# Build up average pixel intensities, casting each image as an array of floats
for im in imlist:
    imarr=numpy.array(Image.open(im),dtype=numpy.float)
    arr=arr+imarr/N

# Round values in array and cast as 8-bit integer
arr=numpy.array(numpy.round(arr),dtype=numpy.uint8)

# Generate, save and preview final image
out=Image.fromarray(arr,mode="RGB")
out.save("Average.png")
out.show()

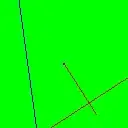
The image below was generated from a sequence of HD video frames using the code above.

Answer 2

I find it difficult to imagine a situation where memory is an issue here, but in the (unlikely) event that you absolutely cannot afford to create the array of floats required for my original answer, you could use PIL's blend function, as suggested by @mHurley as follows:

# Alternative method using PIL blend function
avg=Image.open(imlist[0])
for i in xrange(1,N):
    img=Image.open(imlist[i])
    avg=Image.blend(avg,img,1.0/float(i+1))
avg.save("Blend.png")
avg.show()

You could derive the correct sequence of alpha values, starting with the definition from PIL's blend function:

out = image1 * (1.0 - alpha) + image2 * alpha

Think about applying that function recursively to a vector of numbers (rather than images) to get the mean of the vector. For a vector of length N, you would need N-1 blending operations, with N-1 different values of alpha.

However, it's probably easier to think intuitively about the operations. At each step you want the avg image to contain equal proportions of the source images from earlier steps. When blending the first and second source images, alpha should be 1/2 to ensure equal proportions. When blending the third with the the average of the first two, you would like the new image to be made up of 1/3 of the third image, with the remainder made up of the average of the previous images (current value of avg), and so on.

In principle this new answer, based on blending, should be fine. However I don't know exactly how the blend function works. This makes me worry about how the pixel values are rounded after each iteration.

The image below was generated from 288 source images using the code from my original answer:

On the other hand, this image was generated by repeatedly applying PIL's blend function to the same 288 images:

I hope you can see that the outputs from the two algorithms are noticeably different. I expect this is because of accumulation of small rounding errors during repeated application of Image.blend

I strongly recommend my original answer over this alternative.

Answer 3

One can also use numpy mean function for averaging. The code looks better and works faster.

Here the comparison of timing and results for 700 noisy grayscale images of faces:

def average_img_1(imlist):
    # Assuming all images are the same size, get dimensions of first image
    w,h=Image.open(imlist[0]).size
    N=len(imlist)

    # Create a numpy array of floats to store the average (assume RGB images)
    arr=np.zeros((h,w),np.float)

    # Build up average pixel intensities, casting each image as an array of floats
    for im in imlist:
        imarr=np.array(Image.open(im),dtype=np.float)
        arr=arr+imarr/N
    out = Image.fromarray(arr)
    return out

def average_img_2(imlist):
    # Alternative method using PIL blend function
    N = len(imlist)
    avg=Image.open(imlist[0])
    for i in xrange(1,N):
        img=Image.open(imlist[i])
        avg=Image.blend(avg,img,1.0/float(i+1))
    return avg

def average_img_3(imlist):
    # Alternative method using numpy mean function
    images = np.array([np.array(Image.open(fname)) for fname in imlist])
    arr = np.array(np.mean(images, axis=(0)), dtype=np.uint8)
    out = Image.fromarray(arr)
    return out

average_img_1() 
100 loops, best of 3: 362 ms per loop

average_img_2()
100 loops, best of 3: 340 ms per loop

average_img_3()
100 loops, best of 3: 311 ms per loop

BTW, the results of averaging are quite different. I think the first method lose information during averaging. And the second one has some artifacts.

average_img_1

average_img_2

average_img_3

Answer 4

in case anybody is interested in a blueprint numpy solution (I was actually looking for it), here's the code:

mean_frame = np.mean(([frame for frame in frames]), axis=0)

Answer 5

I would consider creating an array of x by y integers all starting at (0, 0, 0) and then for each pixel in each file add the RGB value in, divide all the values by the number of images and then create the image from that - you will probably find that numpy can help.

Answer 6

I ran into MemoryErrors when trying the method in the accepted answer. I found a way to optimize that seems to produce the same result. Basically, you blend one image at a time, instead of adding them all up and dividing.

N=len(images_to_blend)
avg = Image.open(images_to_blend[0])
for im in images_to_blend: #assuming your list is filenames, not images
    img = Image.open(im)
    avg = Image.blend(avg, img, 1/N)
avg.save(blah)

This does two things, you don't have to have two very dense copies of the image while you're turning the image into an array, and you don't have to use 64-bit floats at all. You get similarly high precision, with smaller numbers. The results APPEAR to be the same, though I'd appreciate if someone checked my math.