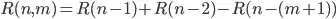12

So, I've seen a few solutions for this problem or similar problems, but I really want to know why mine isn't working. It is much easier to read than a lot of solutions I've found, so I'd love to make it work!

Starting with 1 pair of rabbits, which will begin to reproduce after 2 months. Run for n months, where rabbits die after they have lived for m months. Input of '6 3' should return 4, but it returns 3.

#run for n months, rabbits die after m months.
n, m = input("Enter months to run, and how many months rabbits live, separated by a space ").split() 
n, m = int(n), int(m)
generations = [1, 1, 2] #Seed the sequence with the 1 pair, then in their reproductive month.
def fib(i, j):
    count = 3 #we start at the 3rd generation.
    while (count < i):
        if (count < j):
            generations.append(generations[count-2] + generations[count-1]) #recurrence relation before rabbits start dying
        else:                                                               #is just the fib seq (Fn = Fn-2 + Fn-1)
            generations.append((generations[count-2] + generations[count-1]) - generations[(count-j)])  #Our recurrence relation when rabbits die every month
        count += 1                                                          #is (Fn = Fn-2 + Fn-1 - Fn-j)
    return (generations[count-1])


print (fib(n, m))
print ("Here's how the total population looks by generation: \n" + str(generations))

Thanks =]

Makoto
  • 104,088
  • 27
  • 192
  • 230
spacecadet
  • 251
  • 1
  • 3
  • 9
  • Are you sure you don't have an off-by-one in your while comparison? It returns 4 for input of 6, 3 if you change `while count < i` to `while count <= i`. – lightlike Jun 26 '13 at 01:32
  • To get the last and second last elements, just use `generations[-1]` and `generations[-2]` – John La Rooy Jun 26 '13 at 02:09
  • @lightlike adding the <= makes it run for 7 generations rather than the input 6. As is, it's setting the list like [1, 1, 2, 2, 3, 3] when it should end in 4, not 3. Another example, 7, 4 should return [1, 1, 2, 3, 4, 6, 9]. Instead, we get [1, 1, 2, 3, 4, 6, 8]. **The trend with each test case seems to be that the last number is just off by 1.**. I can cheat and just alter this number before the return...but that's cheating ;) ..unless I know why it's doing this. – spacecadet Jun 26 '13 at 04:35
  • Also worth noting that altering the last element by +1 only works for small inputs. Large inputs are breaking somewhere...and that's much harder to track down. – spacecadet Jun 26 '13 at 04:43
  • If you work through it by hand or print out the program state at each iteration it looks like (6, 3) should give you 3: the equation for the element appended at the last iteration is 2 + 3 - 2. This gives you the same problem for (7, 4) because for both inputs the difference between F(n-j) and F(n-j-1) is 1. What inputs does it 'break' on, and what does it do? – lightlike Jun 26 '13 at 11:30
  • @lightlike By hand, 6, 3 should give 4 (Chart provided with the question). It looks like this, where the numbers represent how many months old a pair of rabbits is. [1][2][3,1][1,2][2,3,1][3,1,1,2] I've noticed an issue in my count variable. It prints like this: Count:..........3, 4, 5, 3 . List :[1, 1, 2, 2, 3, 3] The print (count) statement is within my while loop. As for large input fails, an auto-checker marks wrong on inputs like 88 17, even after I forcibly add +1 to the last element. – spacecadet Jun 26 '13 at 21:35
  • The problem is my algorithm. I went on the assumption that anything alive 3 months ago is dead (true) but have not accounted for things that are not only 1 month old. In other words, I'm subtracting things that are no longer alive, true, but some of those have already died out. – spacecadet Jun 26 '13 at 22:20
  • 10
    You should post your correct answer an an answer, so that you can accept your answer and we can up-vote your answer :) – James Polley Jul 19 '13 at 10:06
  • 3
    @spacecadet, please add an answer and mark it as accepted (You'll even get points for this!). Your question shows up as unanswered, distracting from real unanswered questions. – trapicki Aug 14 '13 at 11:46

5 Answers5

2

This is copied from the answer in SpaceCadets question to help rbump it out of the "unanswered" list of questions.

The two keys here were drawing out the tree to a large number, AND making sure to include a base case check for the first and second generations of deaths (It's -1 in both cases, and then it's something that depends on input).

So 3 potential cases. The regular fib sequence when we don't need to account for deaths, the first and second generations of deaths to initialize our final sequence with the recurrence relation Fn-2 + Fn-1 - Fn-(monthsAlive+1)

I'm certain there's a way to merge 1 or 2 of these checks and make the algorithm more efficient, but as of now it solved a large test case (90, 17) instantly and correctly. So I'm happy.

Lesson learned: Use the entire white-board.

#run for n months, rabbits die after m months.
n, m = input("Enter months to run, and how many months rabbits live, separated by a space ").split() 
n, m = int(n), int(m)
generations = [1, 1] #Seed the sequence with the 1 pair, then in their reproductive month.
def fib(i, j):
    count = 2
    while (count < i):
        if (count < j):
            generations.append(generations[-2] + generations[-1]) #recurrence relation before rabbits start dying (simply fib seq Fn = Fn-2 + Fn-1)
        elif (count == j or count == j+1):
            print ("in base cases for newborns (1st+2nd gen. deaths)") #Base cases for subtracting rabbit deaths (1 death in first 2 death gens)
            generations.append((generations[-2] + generations[-1]) - 1)#Fn = Fn-2 + Fn-1 - 1
        else:
            generations.append((generations[-2] + generations[-1]) - (generations[-(j+1)])) #Our recurrence relation here is Fn-2 + Fn-1 - Fn-(j+1)
        count += 1
    return (generations[-1])


print (fib(n, m))
print ("Here's how the total population looks by generation: \n" + str(generations))
2

Using recursion. 

public static int fibRec(int months, int dieAfter) {
    if(months <= 0) return 0;
    if(months == 1) return 1;
    if(months <= dieAfter)
        return fibRec(months-1, dieAfter) + fibRec(months-2, dieAfter);
    else if (months == dieAfter+1)
        return fibRec(months-1, dieAfter) + fibRec(months-2, dieAfter) - 1;
    else
        return fibRec(months-1, dieAfter) + fibRec(months-2, dieAfter) 
                 - fibRec(months-(dieAfter+1), dieAfter);
}
Red Mercury
  • 3,971
  • 1
  • 26
  • 32
1

There are 2 cases for the recurrence relationship here. Considering n is the number of months the sequence is running for, and m is the number of months a pair is going to live for:

1) If the index in the sequence (zero-based) is less than m:
Normal Fibonacci (Current term = previous term + the one before it).

2) If the index is greater than or equal to m:
Current term = sum of (m - 1) previous terms (ignoring the one immediately before).

Here's an example with a sequence named A and m = 5:
A5 = A0 + A1 + A2 + A3 (4 terms, i.e. m - 1, ignoring the one immediately before)
.
If m = 3 then:
A3 = A0 + A1 (only 2 terms, m - 1)

.

The code below (in Python) has an offset by 2 because of the initial [1, 1] at the beginning of the sequence. 

def mortal_rabbits(n, m):
    sequence = [1, 1]

    for i in range(n - 2):
        new_num = 0
        if i + 2 < m:
            #Normal fibonacci - No deaths yet
            new_num = sequence[i] + sequence[i + 1]
        else:
            #Different reoccurence relation - Accounting for death
            for j in range(m - 1):
                new_num += sequence[i - j]

        sequence.append(new_num)

    return sequence
Abdurrahman
  • 181
  • 2
  • 7
  • You can replace the `for j` loop with `new_num = sum(sequence[i - (m - 2):i + 1])`, which is equally inscrutable. –  Feb 26 '16 at 08:13
1

Ignoring complications, the equation for the number of rabbit pairs in a generation is

rabbit_pairs

If we use a list, this presents a problem because when n == m, we need the value that is at position -1, which is obviously out of bounds.

def rabbit_pairs(n, m):
    sequence = list()
    for i in range(n):
        if i < 2:
            # Normal Fibonacci initialization
            total = 1
            sequence.append(total)
        elif (i < m) or (m == 0):
            # Normal Fibonacci calculation
            total = sequence[i - 1] + sequence[i - 2]
            sequence.append(total)
        elif i == m:
            # Now we need R(n - (m + 1)), but i - (m + 1) < 0, so we have to
            # provide the missing value
            total = sequence[i - 1] + sequence[i - 2] - 1
            sequence.append(total)
        else:
            # i - (m + 1) >= 0, so we can get the value from the sequence
            total = sequence[i - 1] + sequence[i - 2] - sequence[i - (m + 1)]
            sequence.append(total)
    return total
0

Code naively simulating the behaviour in the task, can be faster with touples I guess

def fibm(n,m):
    seq = [[0,0],[0,1],[1,0],[1,1]]
    
    #(old,new)
    for i in range(4,n+1):
        
        new = seq[i-1][0]#new = previous old
        old = seq[i-1][0] + seq[i-1][1] #old = prev old + prev new
        
        if i>m:
            
            old = old - seq[i-m][1] #new from m ago die off
            
        seq.append([old,new])
    return(seq)       
                   
n,m = 95,16

print(sum(fibm(n,m)[-1]))
Ted Archer
  • 1
  • 1