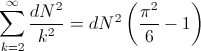Update
I have made an improvement of the algorithm that it takes an average of O(M + N^2) and memory needs of O(M+N). Mainly is the same that the protocol described below, but to calculate the possible factors A,K for ech diference D, I preload a table. This table takes less than a second to be constructed for M=10^7.
I have made a C implementation that takes less than 10minutes to solve N=10^5 diferent random integer elements.
Here is the source code in C: To execute just do: gcc -O3 -o findgeo findgeo.c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <memory.h>
#include <time.h>
struct Factor {
int a;
int k;
struct Factor *next;
};
struct Factor *factors = 0;
int factorsL=0;
void ConstructFactors(int R) {
int a,k,C;
int R2;
struct Factor *f;
float seconds;
clock_t end;
clock_t start = clock();
if (factors) free(factors);
factors = malloc (sizeof(struct Factor) *((R>>1) + 1));
R2 = R>>1 ;
for (a=0;a<=R2;a++) {
factors[a].a= a;
factors[a].k=1;
factors[a].next=NULL;
}
factorsL=R2+1;
R2 = floor(sqrt(R));
for (k=2; k<=R2; k++) {
a=1;
C=a*k*(k+1);
while (C<R) {
C >>= 1;
f=malloc(sizeof(struct Factor));
*f=factors[C];
factors[C].a=a;
factors[C].k=k;
factors[C].next=f;
a++;
C=a*k*(k+1);
}
}
end = clock();
seconds = (float)(end - start) / CLOCKS_PER_SEC;
printf("Construct Table: %f\n",seconds);
}
void DestructFactors() {
int i;
struct Factor *f;
for (i=0;i<factorsL;i++) {
while (factors[i].next) {
f=factors[i].next->next;
free(factors[i].next);
factors[i].next=f;
}
}
free(factors);
factors=NULL;
factorsL=0;
}
int ipow(int base, int exp)
{
int result = 1;
while (exp)
{
if (exp & 1)
result *= base;
exp >>= 1;
base *= base;
}
return result;
}
void findGeo(int **bestSolution, int *bestSolutionL,int *Arr, int L) {
int i,j,D;
int mustExistToBeBetter;
int R=Arr[L-1]-Arr[0];
int *possibleSolution;
int possibleSolutionL=0;
int exp;
int NextVal;
int idx;
int kMax,aMax;
float seconds;
clock_t end;
clock_t start = clock();
kMax = floor(sqrt(R));
aMax = floor(R/2);
ConstructFactors(R);
*bestSolutionL=2;
*bestSolution=malloc(0);
possibleSolution = malloc(sizeof(int)*(R+1));
struct Factor *f;
int *H=malloc(sizeof(int)*(R+1));
memset(H,0, sizeof(int)*(R+1));
for (i=0;i<L;i++) {
H[ Arr[i]-Arr[0] ]=1;
}
for (i=0; i<L-2;i++) {
for (j=i+2; j<L; j++) {
D=Arr[j]-Arr[i];
if (D & 1) continue;
f = factors + (D >>1);
while (f) {
idx=Arr[i] + f->a * f->k - Arr[0];
if ((f->k <= kMax)&& (f->a<aMax)&&(idx<=R)&&H[idx]) {
if (f->k ==1) {
mustExistToBeBetter = Arr[i] + f->a * (*bestSolutionL);
} else {
mustExistToBeBetter = Arr[i] + f->a * f->k * (ipow(f->k,*bestSolutionL) - 1)/(f->k-1);
}
if (mustExistToBeBetter< Arr[L-1]+1) {
idx= floor(mustExistToBeBetter - Arr[0]);
} else {
idx = R+1;
}
if ((idx<=R)&&H[idx]) {
possibleSolution[0]=Arr[i];
possibleSolution[1]=Arr[i] + f->a*f->k;
possibleSolution[2]=Arr[j];
possibleSolutionL=3;
exp = f->k * f->k * f->k;
NextVal = Arr[j] + f->a * exp;
idx=NextVal - Arr[0];
while ( (idx<=R) && H[idx]) {
possibleSolution[possibleSolutionL]=NextVal;
possibleSolutionL++;
exp = exp * f->k;
NextVal = NextVal + f->a * exp;
idx=NextVal - Arr[0];
}
if (possibleSolutionL > *bestSolutionL) {
free(*bestSolution);
*bestSolution = possibleSolution;
possibleSolution = malloc(sizeof(int)*(R+1));
*bestSolutionL=possibleSolutionL;
kMax= floor( pow (R, 1/ (*bestSolutionL) ));
aMax= floor(R / (*bestSolutionL));
}
}
}
f=f->next;
}
}
}
if (*bestSolutionL == 2) {
free(*bestSolution);
possibleSolutionL=0;
for (i=0; (i<2)&&(i<L); i++ ) {
possibleSolution[possibleSolutionL]=Arr[i];
possibleSolutionL++;
}
*bestSolution = possibleSolution;
*bestSolutionL=possibleSolutionL;
} else {
free(possibleSolution);
}
DestructFactors();
free(H);
end = clock();
seconds = (float)(end - start) / CLOCKS_PER_SEC;
printf("findGeo: %f\n",seconds);
}
int compareInt (const void * a, const void * b)
{
return *(int *)a - *(int *)b;
}
int main(void) {
int N=100000;
int R=10000000;
int *A = malloc(sizeof(int)*N);
int *Sol;
int SolL;
int i;
int *S=malloc(sizeof(int)*R);
for (i=0;i<R;i++) S[i]=i+1;
for (i=0;i<N;i++) {
int r = rand() % (R-i);
A[i]=S[r];
S[r]=S[R-i-1];
}
free(S);
qsort(A,N,sizeof(int),compareInt);
/*
int step = floor(R/N);
A[0]=1;
for (i=1;i<N;i++) {
A[i]=A[i-1]+step;
}
*/
findGeo(&Sol,&SolL,A,N);
printf("[");
for (i=0;i<SolL;i++) {
if (i>0) printf(",");
printf("%d",Sol[i]);
}
printf("]\n");
printf("Size: %d\n",SolL);
free(Sol);
free(A);
return EXIT_SUCCESS;
}
Demostration
I will try to demonstrate that the algorithm that I proposed is 
in average for an equally distributed random sequence. I’m not a mathematician and I am not used to do this kind of demonstrations, so please fill free to correct me any error that you can see.
There are 4 indented loops, the two firsts are the N^2 factor. The M is for the calculation of the possible factors table).
The third loop is executed only once in average for each pair. You can see this checking the size of the pre-calculated factors table. It’s size is M when N->inf. So the average steps for each pair is M/M=1.
So the proof happens to check that the forth loop. (The one that traverses the good made sequences is executed less that or equal O(N^2) for all the pairs.
To demonstrate that, I will consider two cases: one where M>>N and other where M ~= N. Where M is the maximum difference of the initial array: M= S(n)-S(1).
For the first case, (M>>N) the probability to find a coincidence is p=N/M. To start a sequence, it must coincide the second and the b+1 element where b is the length of the best sequence until now. So the loop will enter 
times. And the average length of this series (supposing an infinite series) is 
. So the total number of times that the loop will be executed is 
. And this is close to 0 when M>>N. The problem here is when M~=N.
Now lets consider this case where M~=N. Lets consider that b is the best sequence length until now. For the case A=k=1, then the sequence must start before N-b, so the number of sequences will be N-b, and the times that will go for the loop will be a maximum of (N-b)*b.
For A>1 and k=1 we can extrapolate to 
where d is M/N (the average distance between numbers). If we add for all A’s from 1 to dN/b then we see a top limit of:
For the cases where k>=2, we see that the sequence must start before 
, So the loop will enter an average of 
and adding for all As from 1 to dN/k^b, it gives a limit of
Here, the worst case is when b is minimum. Because we are considering minimum series, lets consider a very worst case of b= 2 so the number of passes for the 4th loop for a given k will be less than
.
And if we add all k’s from 2 to infinite will be:
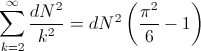
So adding all the passes for k=1 and k>=2, we have a maximum of:
Note that d=M/N=1/p.
So we have two limits, One that goes to infinite when d=1/p=M/N goes to 1 and other that goes to infinite when d goes to infinite. So our limit is the minimum of both, and the worst case is when both equetions cross. So if we solve the equation:
we see that the maximum is when d=1.353
So it is demonstrated that the forth loops will be processed less than 1.55N^2 times in total.
Of course, this is for the average case. For the worst case I am not able to find a way to generate series whose forth loop are higher than O(N^2), and I strongly believe that they does not exist, but I am not a mathematician to prove it.
Old Answer
Here is a solution in average of O((n^2)*cube_root(M)) where M is the difference between the first and last element of the array. And memory requirements of O(M+N).
1.- Construct an array H of length M so that M[i - S[0]]=true if i exists in the initial array and false if it does not exist.
2.- For each pair in the array S[j], S[i] do:
2.1 Check if it can be the first and third elements of a possible solution. To do so, calculate all possible A,K pairs that meet the equation S(i) = S(j) + AK + AK^2. Check this SO question to see how to solve this problem. And check that exist the second element: S[i]+ A*K
2.2 Check also that exist the element one position further that the best solution that we have. For example, if the best solution that we have until now is 4 elements long then check that exist the element A[j] + AK + AK^2 + AK^3 + AK^4
2.3 If 2.1 and 2.2 are true, then iterate how long is this series and set as the bestSolution until now is is longer that the last.
Here is the code in javascript:
function getAKs(A) {
if (A / 2 != Math.floor(A / 2)) return [];
var solution = [];
var i;
var SR3 = Math.pow(A, 1 / 3);
for (i = 1; i <= SR3; i++) {
var B, C;
C = i;
B = A / (C * (C + 1));
if (B == Math.floor(B)) {
solution.push([B, C]);
}
B = i;
C = (-1 + Math.sqrt(1 + 4 * A / B)) / 2;
if (C == Math.floor(C)) {
solution.push([B, C]);
}
}
return solution;
}
function getBestGeometricSequence(S) {
var i, j, k;
var bestSolution = [];
var H = Array(S[S.length-1]-S[0]);
for (i = 0; i < S.length; i++) H[S[i] - S[0]] = true;
for (i = 0; i < S.length; i++) {
for (j = 0; j < i; j++) {
var PossibleAKs = getAKs(S[i] - S[j]);
for (k = 0; k < PossibleAKs.length; k++) {
var A = PossibleAKs[k][0];
var K = PossibleAKs[k][17];
var mustExistToBeBetter;
if (K==1) {
mustExistToBeBetter = S[j] + A * bestSolution.length;
} else {
mustExistToBeBetter = S[j] + A * K * (Math.pow(K,bestSolution.length) - 1)/(K-1);
}
if ((H[S[j] + A * K - S[0]]) && (H[mustExistToBeBetter - S[0]])) {
var possibleSolution=[S[j],S[j] + A * K,S[i]];
exp = K * K * K;
var NextVal = S[i] + A * exp;
while (H[NextVal - S[0]] === true) {
possibleSolution.push(NextVal);
exp = exp * K;
NextVal = NextVal + A * exp;
}
if (possibleSolution.length > bestSolution.length) {
bestSolution = possibleSolution;
}
}
}
}
}
return bestSolution;
}
//var A= [ 1, 2, 3,5,7, 15, 27, 30,31, 81];
var A=[];
for (i=1;i<=3000;i++) {
A.push(i);
}
var sol=getBestGeometricSequence(A);
$("#result").html(JSON.stringify(sol));
You can check the code here: http://jsfiddle.net/6yHyR/1/
I maintain the other solution because I believe that it is still better when M is very big compared to N.
