9

I have the following problem: I need to compute the inclusive scans (e.g. prefix sums) of values based on a tree structure on the GPU. These scans are either from the root node (top-down) or from the leaf nodes (bottom-up). The case of a simple chain is easily handled, but the tree structure makes parallelization rather difficult to implement efficiently.

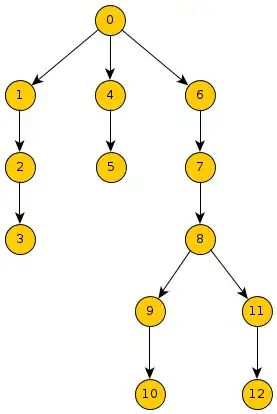
Tree example

For instance, after a top-down inclusive scan, (12) would hold (0)[op](6)[op](7)[op](8)[op](11)[op](12), and for a bottom-up inclusive scan, (8) would hold (8)[op](9)[op](10)[op](11)[op](12), where [op] is a given binary operator (matrix addition, multiplication etc.).

One also needs to consider the following points:

  • For a typical scenario, the length of the different branches should not be too long (~10), with something like 5 to 10 branches, so this is something that will run inside a block and work will be split between the threads. Different blocks will simply handle different values of nodes. This is obviously not optimal regarding occupancy, but this is a constraint on the problem that will be tackled sometime later. For now, I will rely on Instruction-level parallelism.
  • The structure of the graph cannot be changed (it describes an actual system), thus it cannot be balanced (or only by changing the root of the tree, e.g. using (6) as the new root). Nonetheless, a typical tree should not be too unbalanced.
  • I currently use CUDA for GPGPU, so I am open to any CUDA-enabled template library that can solve this issue.
  • Node data is already in global memory and the result will be used by other CUDA kernels, so the objective is just to achieve this without making it a huge bottleneck.
  • There is no "cycle", i.e. branches cannot merge down the tree.
  • The structure of the tree is fixed and set in an initialization phase.
  • A single binary operation can be quite expensive (e.g. multiplication of polynomial matrices, i.e. each element is a polynomial of a given order).

In this case, what would be the "best" data structure (for the tree structure) and the best algorithms (for the inclusive scans/prefix sums) to solve this problem?

Community
  • 1
  • 1
BenC
  • 8,729
  • 3
  • 49
  • 68
  • 4
    Awesome question. We need more of this type of question and fewer of the basic bug fixing questions we get all the time. – Roger Dahl Oct 03 '13 at 14:06
  • The problem size is so small (10 branches x 10 notes/branch). I'm guessing even if you use only 1 thread to compute all the prefix-sums for all the nodes, the time cost can be ignored compared to other parts of the code that runs on the GPU. – kangshiyin Oct 03 '13 at 14:16
  • @Eric: the thing is, each node actually handles quite a lot of computation (e.g. polynomial matrices that need to be multiplied), so the sequential algorithm becomes a bottleneck. I tried this with the simple chains, and a smarter logarithmic approach provided a nonnegligible speedup. – BenC Oct 03 '13 at 14:20
  • Do you mean the `AssociateOperator binary_op` as defined [here](http://thrust.github.io/doc/group__prefixsums.html#ga7109170b96a48fab736e52b75f423464) is not a simple scale plus operator? otherwise the computation with in a node can be calculated before the prefix sums. – kangshiyin Oct 03 '13 at 14:40
  • @Eric: for instance, each node holds a transformation matrix (from the previous node to the current node), and you want the transformation from the root to each node. Thus, for each computation step, you need data from 2 different nodes to compute the transformation from one node to the other. – BenC Oct 03 '13 at 14:50
  • In your transformation example, the `binary_op` should be matrix multiplication, right? If a single `binary_op` can occupy the whole GPU, then do multiple `binary_op` in parallel will be impossible. So your problem is, the `binary_op` has large time cost but not large enough to fully utilize the GPU. Am I correct? I still think you should provide more details about the nodes and your scan operation, rather than a single `+` operator. – kangshiyin Oct 03 '13 at 15:24
  • @Eric: it does not occupy the whole GPU (unless I use too much shared memory for the prefix sum), but it is expensive nonetheless. Computation is quite suitable for loop unrolling which helps increasing performance. Thus, a sequential method would be really slow, and a divide-and-conquer approach would limit that performance drop if done in a smart way. I will add some more details to my question though. – BenC Oct 03 '13 at 15:48

4 Answers4

3

Probably a harebrained idea, but imagine that you insert nodes of 0 value into the tree, in such a way that you get a 2D matrix. For instance, there would be 3 zero value nodes below the 5 node in your example. Then use one thread to travel each level of the matrix horizontally. For the top-down prefix sum, offset the threads in such a way that each lower thread is delayed by the maximum number of branches the tree can have in that location. So, you get a "wave" with a slanted edge running over the matrix. The upper threads, being further along, calculate those nodes in time for them to be processed further by threads running further down. You would need the same number of threads as the tree is deep.

Roger Dahl
  • 15,132
  • 8
  • 62
  • 82
  • This reminds me of something I did when computing the gradient of the partial product. I ended up generating a parallel computing plan on the CPU that stores relevant array indices used to generate a temporary array that contained all the possible partial products. Then, at each GPU computing step, a varying number of threads would compute values on sliding diagonals based on these indices to fill the array (wavefront-style). I was concerned about memory coalescence, but it did not seem to matter that much in this scenario. Anyhow, I'll try to evaluate your suggestion as soon as possible. – BenC Oct 03 '13 at 17:29
3

I think parallel prefix scan may not suitable for your case because:

parallel prefix scan algorithm will increase the total number of [op], in your link of prefix sum, a 16-input parallel prefix scan requires 26 [op], while a sequential version only need 15. parallel algorithm performs better is based on a assumption that there's enough hardware resources to run multiple [op] in parallel.

You could evaluate the cost of your [op] before try the parallel prefix scan.

On the other hand, since the size of the tree is small, I think you could simply consider your tree as 4 (number of the leaf nodes) independent simple chains, and use concurrent kernel execution to improve the performance of these 4 prefix scan kernels

0-1-2-3
0-4-5
0-6-7-8-9-10
0-6-7-8-11-12
kangshiyin
  • 9,681
  • 1
  • 17
  • 29
  • Concerning your last comment on concurrent kernel execution, this is indeed something I considered for the "root to leaves" problem. However, the "leaves to root" problem would require the use of atomic operations since some of the branches will modify identical nodes at the same time if they have the same length. The number of branches should be quite low so this may not influence the performance much though. – BenC Oct 03 '13 at 16:49
  • For the bottom-up path, do you mean you need store 2 sums for nodes as `(8)`? one is 10-9-8, the other is 12-11-8 ? I would suggest out-place operation if that's true. – kangshiyin Oct 03 '13 at 16:58
  • No, just one (as explained in my question). It's the sum of all the lower nodes in the given branch. – BenC Oct 03 '13 at 17:04
  • 1
    erh.. Then this is totally not a prefix scan problem, which can be defined by the only **binary** `[op]` – kangshiyin Oct 03 '13 at 17:08
  • Not exactly, but I do not think that there is a dedicated word for that. This is what makes the bottom-up problem a bit more complicated in my opinion. – BenC Oct 03 '13 at 17:11
  • If you can do 1 `[op]` per kernel, some host side strategy like [wavefront](http://software.intel.com/sites/products/documentation/doclib/tbb_sa/help/tbb_userguide/Design_Patterns/Wavefront.htm) should work – kangshiyin Oct 03 '13 at 17:24
0

I think in Kepler GK110 architecture, you can invoke kernels recursively, which they call dynamic parallelism. So, if you need to compute the sum of the values at each node of the tree, dynamic parallelism would help. However, the depth of recursion might be a constraint.

Bharat
  • 2,139
  • 2
  • 16
  • 35
  • I haven't tried dynamic parallelism yet, as I only have a CC 3.0 device. I don't know how it would respond to limited recursion like this. – BenC Oct 07 '13 at 13:52
0

My first impression is that you could organize the tree nodes in a 1 dimensional array, similar to what Eric suggested. And then you could do a Segmented Prefix Sum Scan (http://en.wikipedia.org/wiki/Segmented_scan) over that array.

Using your tree nodes as an example, the 1-dim array would look like:

0-1-2-3-0-4-5-0-6-7-8-9-10-0-6-7-8-11-12

And then you would have a parallel array of flags indicating where a new list begins (by list I mean a sequence beginning at the root and ending at a leaf node):

1-0-0-0-1-0-0-1-0-0-0-0- 0-1-0-0-0- 0- 0

For the bottom-up case, you could create a separate segment-flag array like so:

0-0-0-1-0-0-1-0-0-0-0-0- 1-0-0-0-0- 0- 1

and traverse it in reverse order using the same algorithm.

As for how to implement a Segmented Prefix Scan, I haven't implemented one myself but I found a couple of references that might be informative on how to do it: http://www.cs.cmu.edu/afs/cs/academic/class/15418-s12/www/lectures/24_algorithms.pdf and http://www.cs.ucdavis.edu/research/tech-reports/2011/CSE-2011-4.pdf (see page 23)

MorbidFuzzball
  • 71
  • 3
  • Indeed, a segmented prefix sum could work I suppose. There's also one implemented in [Thrust](http://thrust.github.io/doc/group__segmentedprefixsums.html). This just means some redundant computation and extra memory storage (e.g. the `0-6-7-8` part that is computed twice for the two lowest branches). – BenC Oct 07 '13 at 14:04
  • Yeah, I noticed the duplicate segments. Perhaps a system could be devised to eliminate the duplicates. For example, before giving the array to a segmented scan, first search for repeated segments, and pull out the repeated sections and replace them with some kind of indicator that will let you reconstruct the complete list at the end. In a sense, it would be like compressing the input list, and then decompressing it at the end. – MorbidFuzzball Oct 07 '13 at 18:05
  • Also, this does not necessarily solve the reverse problem where multiple inputs (going up from the leaves) influence one "merging" node, thus leading to possible WAW hazards. – BenC Oct 08 '13 at 15:57