Math: Is this k-means clustering?

Question

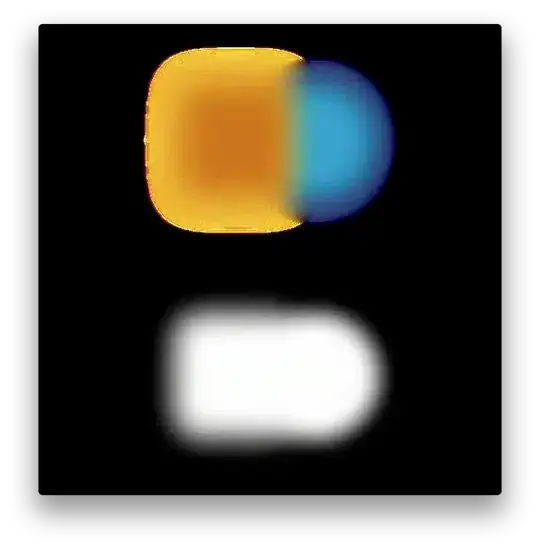
enter image description here

Hello! I have some points on a line. These points do not have an Y dimension, only an X dimension. I only placed them in an Y dimension because this wanted to be able to place multiple dots on the same spot.

I would like find n centroids (spots with the most density).

I placed for example centroids (=green lines) to show what I mean. These examplary centroids were not calculated, I only placed them guessing where they would be.

Before I dive into the math, I would like to know if this is can be solved with k-means-clustering, or if I am going in the wrong direction.

Thank you.

IMO you're just going on the wrong web site! :) Try with http://math.stackexchange.com/ — Adriano Repetti, Oct 17 '13 at 10:00
the image does not work (it gives a red cross), but with a one dimensional data set I guess you could make clusters and then draw the points per cluster (i.e. cluster as the x-axis and points as the Y axis with maybe a line on the x axis to describe the centroids?) see also: http://stackoverflow.com/questions/7869609/cluster-one-dimensional-data-optimally — Carst, Oct 17 '13 at 10:02

score 0 · Answer 1 · answered Oct 17 '13 at 11:18

K-means is rather sensitive to noise, and you seem to have a lot of noise. But yes, it may work to some extend. Plus, it does not exploit that your data is just 1 dimensional.

However, it sounds to me as if you want to do some very primitive mode seeking. In 1D, the most appropriate approach for you is Kernel Density Estimation, and then choose the local density maxima.

"Cluster analysis" sure sounds much more fancy, but nevertheless classical statistic "KDE" will likely produce much better results. In particular, you don't have to fix "k" beforehand, and it will be much more robust wrt. noise.

score 0 · Answer 2 · edited May 08 '14 at 19:59

You can use K-means and actually the implementation is so easy:

Select the number of clusters you want
Select k points randomly (You can repeat this for avoiding local optimum)
Find the distance of each other points to these k centers
Assign the points to the nearest center
For each set of points calculate the average
If the average is changing, move the center of the clusters to the new averages and go to 3
Otherwise finish

Or you can use matlab to do this for you:

k = 2;
rng('default') % For reproducibility
X = [randn(100,1)+ones(100,1);...
     randn(100,1)-ones(100,1)];

opts = statset('Display','final');
[idx,ctrs] = kmeans(X,k,'Distance','city','Replicates',5,'Options',opts);

plot(X(idx==1,1),X(idx==1,1),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,1),'b.','MarkerSize',12)
plot(ctrs(:,1),ctrs(:,1),'kx','MarkerSize',12,'LineWidth',2)
plot(ctrs(:,1),ctrs(:,1),'ko','MarkerSize',12,'LineWidth',2)
legend('Cluster 1','Cluster 2','Centroids','Location','NW')
hold off

I put the result in diagonal to show it better, but the real data is 1D:

enter image description here

Math: Is this k-means clustering?

2 Answers2