What is the BigO of linear regression?

Question

How large a system is it reasonable to attempt to do a linear regression on?

Specifically: I have a system with ~300K sample points and ~1200 linear terms. Is this computationally feasible?

Answer 1

The linear regression is computed as (X'X)^-1 X'Y.

If X is an (n x k) matrix:

1. (X' X) takes O(n*k^2) time and produces a (k x k) matrix

2. The matrix inversion of a (k x k) matrix takes O(k^3) time

3. (X' Y) takes O(n*k^2) time and produces a (k x k) matrix

4. The final matrix multiplication of two (k x k) matrices takes O(k^3) time

So the Big-O running time is O(k^2*(n + k)).

See also: http://en.wikipedia.org/wiki/Computational_complexity_of_mathematical_operations#Matrix_algebra

If you get fancy it looks like you can get the time down to O(k^2*(n+k^0.376)) with the Coppersmith–Winograd algorithm.

Answer 2

You can express this as a matrix equation:

where the matrix is 300K rows and 1200 columns, the coefficient vector is 1200x1, and the RHS vector 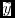is 1200x1.

If you multiply both sides by the transpose of the matrix 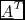, you have a system of equations for the unknowns that's 1200x1200. You can use LU decomposition or any other algorithm you like to solve for the coefficients. (This is what least squares is doing.)

So the Big-O behavior is something like O(mmn), where m = 300K and n = 1200. You'd account for the transpose, the matrix multiplication, the LU decomposition, and the forward-back substitution to get the coefficients.

Answer 3

The linear regression is computed as (X'X)^-1 X'y.

As far as I learned, y is a vector of results (or in other words: dependant variables).

Therefore, if X is an (n × m) matrix and y is an (n × 1) matrix:

1. The transposing of a (n × m) matrix takes O(n⋅m) time and produces a (m × n) matrix
2. (X' X) takes O(n⋅m²) time and produces a (m × m) matrix
3. The matrix inversion of a (m × m) matrix takes O(m³) time
4. (X' y) takes O(n⋅m) time and produces a (m × 1) matrix
5. The final matrix multiplication of a (m × m) and a (m x 1) matrices takes O(m²) time

So the Big-O running time is O(n⋅m + n⋅m² + m³ + n⋅m + m²).

Now, we know that:

• m² ≤ m³
• n⋅m ≤ n⋅m²

so asymptotically, the actual Big-O running time is O(n⋅m² + m³) = O(m²(n + m)).

And that's what we have from http://en.wikipedia.org/wiki/Computational_complexity_of_mathematical_operations#Matrix_algebra

But, we know that there's a significant difference between the case n → ∞ and m → ∞. https://en.wikipedia.org/wiki/Big_O_notation#Multiple_variables

So which one should we choose? Obviously it's the number of observations which is more likely to grow, rather than the number of attributes. So my conclusion is that if we assume that the number of attributes remains constant, we can ignore the m terms and that's a relief because the time complexity of a multivariate linear regression becomes a mere linear O(n). On the other hand, we can expect our computing time explodes by a large value when the number of attributes increase substantially.

Answer 4

The linear regression of closed-form model is computed as follow: derivative of

RSS(W) = -2H^t (y-HW)

So, we solve for

-2H^t (y-HW) = 0

Then, the W value is

W = (H^t H)^-1 H^2 y

where: W: is the vector of expected weights H: is the features matrix N*D where N is the number of observations, and D is the number of features y: is the actual value

Then, the complexity of

H^t H is n D^2

The complexity of the transpose is D^3

So, The complexity of

(H^t H)^-1 is n * D^2 + D^3