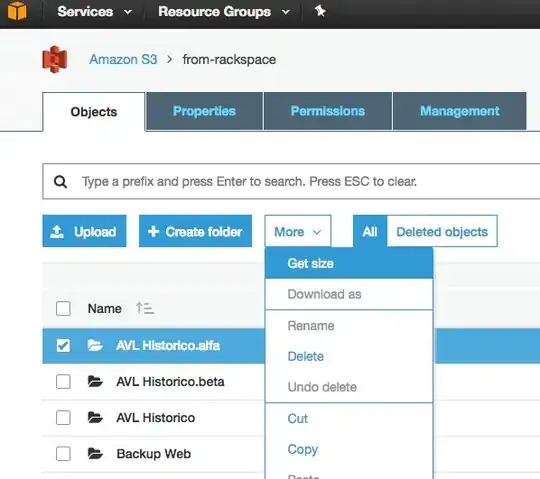
To plot a normal distribution curve in R we can use:
(x = seq(-4,4, length=100))
y = dnorm(x)
plot(x, y)
If dnorm calculates y as a function of x, does R have a function that calculates x as a function of y? If not what is the best way to approach this?