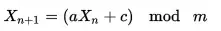Unique (non-repeating) random numbers in O(1)?

Question

I'd like to generate unique random numbers between 0 and 1000 that never repeat (i.e. 6 doesn't show up twice), but that doesn't resort to something like an O(N) search of previous values to do it. Is this possible?

Answer 1

Initialize an array of 1001 integers with the values 0-1000 and set a variable, max, to the current max index of the array (starting with 1000). Pick a random number, r, between 0 and max, swap the number at the position r with the number at position max and return the number now at position max. Decrement max by 1 and continue. When max is 0, set max back to the size of the array - 1 and start again without the need to reinitialize the array.

Update: Although I came up with this method on my own when I answered the question, after some research I realize this is a modified version of Fisher-Yates known as Durstenfeld-Fisher-Yates or Knuth-Fisher-Yates. Since the description may be a little difficult to follow, I have provided an example below (using 11 elements instead of 1001):

Array starts off with 11 elements initialized to array[n] = n, max starts off at 10:

+--+--+--+--+--+--+--+--+--+--+--+
| 0| 1| 2| 3| 4| 5| 6| 7| 8| 9|10|
+--+--+--+--+--+--+--+--+--+--+--+
                                ^
                               max    

At each iteration, a random number r is selected between 0 and max, array[r] and array[max] are swapped, the new array[max] is returned, and max is decremented:

max = 10, r = 3
           +--------------------+
           v                    v
+--+--+--+--+--+--+--+--+--+--+--+
| 0| 1| 2|10| 4| 5| 6| 7| 8| 9| 3|
+--+--+--+--+--+--+--+--+--+--+--+

max = 9, r = 7
                       +-----+
                       v     v
+--+--+--+--+--+--+--+--+--+--+--+
| 0| 1| 2|10| 4| 5| 6| 9| 8| 7: 3|
+--+--+--+--+--+--+--+--+--+--+--+

max = 8, r = 1
     +--------------------+
     v                    v
+--+--+--+--+--+--+--+--+--+--+--+
| 0| 8| 2|10| 4| 5| 6| 9| 1: 7| 3|
+--+--+--+--+--+--+--+--+--+--+--+

max = 7, r = 5
                 +-----+
                 v     v
+--+--+--+--+--+--+--+--+--+--+--+
| 0| 8| 2|10| 4| 9| 6| 5: 1| 7| 3|
+--+--+--+--+--+--+--+--+--+--+--+

...

After 11 iterations, all numbers in the array have been selected, max == 0, and the array elements are shuffled:

+--+--+--+--+--+--+--+--+--+--+--+
| 4|10| 8| 6| 2| 0| 9| 5| 1| 7| 3|
+--+--+--+--+--+--+--+--+--+--+--+

At this point, max can be reset to 10 and the process can continue.

Answer 2

You can do this:

1. Create a list, 0..1000.
2. Shuffle the list. (See Fisher-Yates shuffle for a good way to do this.)
3. Return numbers in order from the shuffled list.

So this doesn't require a search of old values each time, but it still requires O(N) for the initial shuffle. But as Nils pointed out in comments, this is amortised O(1).

Answer 3

Use a Maximal Linear Feedback Shift Register.

It's implementable in a few lines of C and at runtime does little more than a couple test/branches, a little addition and bit shifting. It's not random, but it fools most people.

Answer 4

You could use Format-Preserving Encryption to encrypt a counter. Your counter just goes from 0 upwards, and the encryption uses a key of your choice to turn it into a seemingly random value of whatever radix and width you want. E.g. for the example in this question: radix 10, width 3.

Block ciphers normally have a fixed block size of e.g. 64 or 128 bits. But Format-Preserving Encryption allows you to take a standard cipher like AES and make a smaller-width cipher, of whatever radix and width you want, with an algorithm which is still cryptographically robust.

It is guaranteed to never have collisions (because cryptographic algorithms create a 1:1 mapping). It is also reversible (a 2-way mapping), so you can take the resulting number and get back to the counter value you started with.

This technique doesn't need memory to store a shuffled array etc, which can be an advantage on systems with limited memory.

AES-FFX is one proposed standard method to achieve this. I've experimented with some basic Python code which is based on the AES-FFX idea, although not fully conformant--see Python code here. It can e.g. encrypt a counter to a random-looking 7-digit decimal number, or a 16-bit number. Here is an example of radix 10, width 3 (to give a number between 0 and 999 inclusive) as the question stated:

000   733
001   374
002   882
003   684
004   593
005   578
006   233
007   811
008   072
009   337
010   119
011   103
012   797
013   257
014   932
015   433
...   ...

To get different non-repeating pseudo-random sequences, change the encryption key. Each encryption key produces a different non-repeating pseudo-random sequence.

Answer 5

You could use A Linear Congruential Generator. Where m (the modulus) would be the nearest prime bigger than 1000. When you get a number out of the range, just get the next one. The sequence will only repeat once all elements have occurred, and you don't have to use a table. Be aware of the disadvantages of this generator though (including lack of randomness).

Answer 6

I think that Linear congruential generator would be the simplest solution.

and there are only 3 restrictions on the a, c and m values

1. m and c are relatively prime,
2. a-1 is divisible by all prime factors of m
3. a-1 is divisible by 4 if m is divisible by 4

PS the method was mentioned already but the post has a wrong assumptions about the constant values. The constants below should work fine for your case

In your case you may use a = 1002, c = 757, m = 1001

X = (1002 * X + 757) mod 1001

Answer 7

For low numbers like 0...1000, creating a list that contains all the numbers and shuffling it is straight forward. But if the set of numbers to draw from is very large there's another elegant way: You can build a pseudorandom permutation using a key and a cryptographic hash function. See the following C++-ish example pseudo code:

unsigned randperm(string key, unsigned bits, unsigned index) {
  unsigned half1 =  bits    / 2;
  unsigned half2 = (bits+1) / 2;
  unsigned mask1 = (1 << half1) - 1;
  unsigned mask2 = (1 << half2) - 1;
  for (int round=0; round<5; ++round) {
    unsigned temp = (index >> half1);
    temp = (temp << 4) + round;
    index ^= hash( key + "/" + int2str(temp) ) & mask1;
    index = ((index & mask2) << half1) | ((index >> half2) & mask1);
  }
  return index;
}

Here, hash is just some arbitrary pseudo random function that maps a character string to a possibly huge unsigned integer. The function randperm is a permutation of all numbers within 0...pow(2,bits)-1 assuming a fixed key. This follows from the construction because every step that changes the variable index is reversible. This is inspired by a Feistel cipher.

Answer 8

You may use my Xincrol algorithm described here:

http://openpatent.blogspot.co.il/2013/04/xincrol-unique-and-random-number.html

This is a pure algorithmic method of generating random but unique numbers without arrays, lists, permutations or heavy CPU load.

Latest version allows also to set the range of numbers, For example, if I want unique random numbers in range of 0-1073741821.

I've practically used it for

• MP3 player which plays every song randomly, but only once per album/directory
• Pixel wise video frames dissolving effect (fast and smooth)
• Creating a secret "noise" fog over image for signatures and markers (steganography)
• Data Object IDs for serialization of huge amount of Java objects via Databases
• Triple Majority memory bits protection
• Address+value encryption (every byte is not just only encrypted but also moved to a new encrypted location in buffer). This really made cryptanalysis fellows mad on me :-)
• Plain Text to Plain Like Crypt Text encryption for SMS, emails etc.
• My Texas Hold`em Poker Calculator (THC)
• Several of my games for simulations, "shuffling", ranking
• more

It is open, free. Give it a try...

Answer 9

You don't even need an array to solve this one.

You need a bitmask and a counter.

Initialize the counter to zero and increment it on successive calls. XOR the counter with the bitmask (randomly selected at startup, or fixed) to generate a psuedorandom number. If you can't have numbers that exceed 1000, don't use a bitmask wider than 9 bits. (In other words, the bitmask is an integer not above 511.)

Make sure that when the counter passes 1000, you reset it to zero. At this time you can select another random bitmask — if you like — to produce the same set of numbers in a different order.

Answer 10

Here's some code I typed up that uses the logic of the first solution. I know this is "language agnostic" but just wanted to present this as an example in C# in case anyone is looking for a quick practical solution.

// Initialize variables
Random RandomClass = new Random();
int RandArrayNum;
int MaxNumber = 10;
int LastNumInArray;
int PickedNumInArray;
int[] OrderedArray = new int[MaxNumber];      // Ordered Array - set
int[] ShuffledArray = new int[MaxNumber];     // Shuffled Array - not set

// Populate the Ordered Array
for (int i = 0; i < MaxNumber; i++)                  
{
    OrderedArray[i] = i;
    listBox1.Items.Add(OrderedArray[i]);
}

// Execute the Shuffle                
for (int i = MaxNumber - 1; i > 0; i--)
{
    RandArrayNum = RandomClass.Next(i + 1);         // Save random #
    ShuffledArray[i] = OrderedArray[RandArrayNum];  // Populting the array in reverse
    LastNumInArray = OrderedArray[i];               // Save Last Number in Test array
    PickedNumInArray = OrderedArray[RandArrayNum];  // Save Picked Random #
    OrderedArray[i] = PickedNumInArray;             // The number is now moved to the back end
    OrderedArray[RandArrayNum] = LastNumInArray;    // The picked number is moved into position
}

for (int i = 0; i < MaxNumber; i++)                  
{
    listBox2.Items.Add(ShuffledArray[i]);
}

Answer 11

The question How do you efficiently generate a list of K non-repeating integers between 0 and an upper bound N is linked as a duplicate - and if you want something that is O(1) per generated random number (with no O(n) startup cost)) there is a simple tweak of the accepted answer.

Create an empty unordered map (an empty ordered map will take O(log k) per element) from integer to integer - instead of using an initialized array. Set max to 1000 if that is the maximum,

1. Pick a random number, r, between 0 and max.
2. Ensure that both map elements r and max exist in the unordered map. If they don't exist create them with a value equal to their index.
3. Swap elements r and max
4. Return element max and decrement max by 1 (if max goes negative you are done).
5. Back to step 1.

The only difference compared with using an initialized array is that the initialization of elements is postponed/skipped - but it will generate the exact same numbers from the same PRNG.

Answer 12

This method results appropiate when the limit is high and you only want to generate a few random numbers.

#!/usr/bin/perl

($top, $n) = @ARGV; # generate $n integer numbers in [0, $top)

$last = -1;
for $i (0 .. $n-1) {
    $range = $top - $n + $i - $last;
    $r = 1 - rand(1.0)**(1 / ($n - $i));
    $last += int($r * $range + 1);
    print "$last ($r)\n";
}

Note that the numbers are generated in ascending order, but you can shuffle then afterwards.

Answer 13

public static int[] randN(int n, int min, int max)
{
    if (max <= min)
        throw new ArgumentException("Max need to be greater than Min");
    if (max - min < n)
        throw new ArgumentException("Range needs to be longer than N");

    var r = new Random();

    HashSet<int> set = new HashSet<int>();

    while (set.Count < n)
    {
        var i = r.Next(max - min) + min;
        if (!set.Contains(i))
            set.Add(i);
    }

    return set.ToArray();
}

N Non Repeating random numbers will be of O(n) complexity, as required.
Note: Random should be static with thread safety applied.

Answer 14

Here is some sample COBOL code you can play around with.
I can send you RANDGEN.exe file so you can play with it to see if it does want you want.

   IDENTIFICATION DIVISION.
   PROGRAM-ID.  RANDGEN as "ConsoleApplication2.RANDGEN".
   AUTHOR.  Myron D Denson.
   DATE-COMPILED.
  * ************************************************************** 
  *  SUBROUTINE TO GENERATE RANDOM NUMBERS THAT ARE GREATER THAN
  *    ZERO AND LESS OR EQUAL TO THE RANDOM NUMBERS NEEDED WITH NO
  *    DUPLICATIONS.  (CALL "RANDGEN" USING RANDGEN-AREA.)
  *     
  *  CALLING PROGRAM MUST HAVE A COMPARABLE LINKAGE SECTION
  *    AND SET 3 VARIABLES PRIOR TO THE FIRST CALL IN RANDGEN-AREA     
  *
  *    FORMULA CYCLES THROUGH EVERY NUMBER OF 2X2 ONLY ONCE. 
  *    RANDOM-NUMBERS FROM 1 TO RANDOM-NUMBERS-NEEDED ARE CREATED 
  *    AND PASSED BACK TO YOU.
  *
  *  RULES TO USE RANDGEN:
  *
  *    RANDOM-NUMBERS-NEEDED > ZERO 
  *     
  *    COUNT-OF-ACCESSES MUST = ZERO FIRST TIME CALLED.
  *         
  *    RANDOM-NUMBER = ZERO, WILL BUILD A SEED FOR YOU
  *    WHEN COUNT-OF-ACCESSES IS ALSO = 0 
  *     
  *    RANDOM-NUMBER NOT = ZERO, WILL BE NEXT SEED FOR RANDGEN
  *    (RANDOM-NUMBER MUST BE <= RANDOM-NUMBERS-NEEDED)       
  *     
  *    YOU CAN PASS RANDGEN YOUR OWN RANDOM-NUMBER SEED
  *     THE FIRST TIME YOU USE RANDGEN.
  *     
  *    BY PLACING A NUMBER IN RANDOM-NUMBER FIELD
  *      THAT FOLLOWES THESE SIMPLE RULES:
  *        IF COUNT-OF-ACCESSES = ZERO AND 
  *        RANDOM-NUMBER > ZERO AND 
  *        RANDOM-NUMBER <= RANDOM-NUMBERS-NEEDED
  *       
  *    YOU CAN LET RANDGEN BUILD A SEED FOR YOU
  *     
  *      THAT FOLLOWES THESE SIMPLE RULES:
  *        IF COUNT-OF-ACCESSES = ZERO AND 
  *        RANDOM-NUMBER = ZERO AND 
  *        RANDOM-NUMBER-NEEDED > ZERO  
  *         
  *     TO INSURING A DIFFERENT PATTERN OF RANDOM NUMBERS
  *        A LOW-RANGE AND HIGH-RANGE IS USED TO BUILD
  *        RANDOM NUMBERS.
  *        COMPUTE LOW-RANGE =
  *             ((SECONDS * HOURS * MINUTES * MS) / 3).         
  *        A HIGH-RANGE = RANDOM-NUMBERS-NEEDED + LOW-RANGE
  *        AFTER RANDOM-NUMBER-BUILT IS CREATED 
  *        AND IS BETWEEN LOW AND HIGH RANGE
  *        RANDUM-NUMBER = RANDOM-NUMBER-BUILT - LOW-RANGE
  *               
  * **************************************************************         
   ENVIRONMENT DIVISION.
   INPUT-OUTPUT SECTION.
   FILE-CONTROL.
   DATA DIVISION.
   FILE SECTION.
   WORKING-STORAGE SECTION.
   01  WORK-AREA.
       05  X2-POWER                     PIC 9      VALUE 2. 
       05  2X2                          PIC 9(12)  VALUE 2 COMP-3.
       05  RANDOM-NUMBER-BUILT          PIC 9(12)  COMP.
       05  FIRST-PART                   PIC 9(12)  COMP.
       05  WORKING-NUMBER               PIC 9(12)  COMP.
       05  LOW-RANGE                    PIC 9(12)  VALUE ZERO.
       05  HIGH-RANGE                   PIC 9(12)  VALUE ZERO.
       05  YOU-PROVIDE-SEED             PIC X      VALUE SPACE.
       05  RUN-AGAIN                    PIC X      VALUE SPACE.
       05  PAUSE-FOR-A-SECOND           PIC X      VALUE SPACE.   
   01  SEED-TIME.
       05  HOURS                        PIC 99.
       05  MINUTES                      PIC 99.
       05  SECONDS                      PIC 99.
       05  MS                           PIC 99. 
  *
  * LINKAGE SECTION.
  *  Not used during testing  
   01  RANDGEN-AREA.
       05  COUNT-OF-ACCESSES            PIC 9(12) VALUE ZERO.
       05  RANDOM-NUMBERS-NEEDED        PIC 9(12) VALUE ZERO.
       05  RANDOM-NUMBER                PIC 9(12) VALUE ZERO.
       05  RANDOM-MSG                   PIC X(60) VALUE SPACE.
  *    
  * PROCEDURE DIVISION USING RANDGEN-AREA.
  * Not used during testing 
  *  
   PROCEDURE DIVISION.
   100-RANDGEN-EDIT-HOUSEKEEPING.
       MOVE SPACE TO RANDOM-MSG. 
       IF RANDOM-NUMBERS-NEEDED = ZERO
         DISPLAY 'RANDOM-NUMBERS-NEEDED ' NO ADVANCING
         ACCEPT RANDOM-NUMBERS-NEEDED.
       IF RANDOM-NUMBERS-NEEDED NOT NUMERIC 
         MOVE 'RANDOM-NUMBERS-NEEDED NOT NUMERIC' TO RANDOM-MSG
           GO TO 900-EXIT-RANDGEN.
       IF RANDOM-NUMBERS-NEEDED = ZERO
         MOVE 'RANDOM-NUMBERS-NEEDED = ZERO' TO RANDOM-MSG
           GO TO 900-EXIT-RANDGEN.
       IF COUNT-OF-ACCESSES NOT NUMERIC
         MOVE 'COUNT-OF-ACCESSES NOT NUMERIC' TO RANDOM-MSG
           GO TO 900-EXIT-RANDGEN.
       IF COUNT-OF-ACCESSES GREATER THAN RANDOM-NUMBERS-NEEDED
         MOVE 'COUNT-OF-ACCESSES > THAT RANDOM-NUMBERS-NEEDED'
           TO RANDOM-MSG
           GO TO 900-EXIT-RANDGEN.
       IF YOU-PROVIDE-SEED = SPACE AND RANDOM-NUMBER = ZERO
         DISPLAY 'DO YOU WANT TO PROVIDE SEED  Y OR N: '
           NO ADVANCING
           ACCEPT YOU-PROVIDE-SEED.  
       IF RANDOM-NUMBER = ZERO AND
          (YOU-PROVIDE-SEED = 'Y' OR 'y')
         DISPLAY 'ENTER SEED ' NO ADVANCING
         ACCEPT RANDOM-NUMBER. 
       IF RANDOM-NUMBER NOT NUMERIC
         MOVE 'RANDOM-NUMBER NOT NUMERIC' TO RANDOM-MSG
         GO TO 900-EXIT-RANDGEN.
   200-RANDGEN-DATA-HOUSEKEEPING.      
       MOVE FUNCTION CURRENT-DATE (9:8) TO SEED-TIME.
       IF COUNT-OF-ACCESSES = ZERO
         COMPUTE LOW-RANGE =
                ((SECONDS * HOURS * MINUTES * MS) / 3).
       COMPUTE RANDOM-NUMBER-BUILT = RANDOM-NUMBER + LOW-RANGE.  
       COMPUTE HIGH-RANGE = RANDOM-NUMBERS-NEEDED + LOW-RANGE.
       MOVE X2-POWER TO 2X2.             
   300-SET-2X2-DIVISOR.
       IF 2X2 < (HIGH-RANGE + 1) 
          COMPUTE 2X2 = 2X2 * X2-POWER
           GO TO 300-SET-2X2-DIVISOR.    
  * *********************************************************         
  *  IF FIRST TIME THROUGH AND YOU WANT TO BUILD A SEED.    *
  * ********************************************************* 
       IF COUNT-OF-ACCESSES = ZERO AND RANDOM-NUMBER = ZERO
          COMPUTE RANDOM-NUMBER-BUILT =
                ((SECONDS * HOURS * MINUTES * MS) + HIGH-RANGE).
       IF COUNT-OF-ACCESSES = ZERO        
         DISPLAY 'SEED TIME ' SEED-TIME 
               ' RANDOM-NUMBER-BUILT ' RANDOM-NUMBER-BUILT 
               ' LOW-RANGE  ' LOW-RANGE.          
  * *********************************************     
  *    END OF BUILDING A SEED IF YOU WANTED TO  * 
  * *********************************************               
  * ***************************************************
  * THIS PROCESS IS WHERE THE RANDOM-NUMBER IS BUILT  *  
  * ***************************************************   
   400-RANDGEN-FORMULA.
       COMPUTE FIRST-PART = (5 * RANDOM-NUMBER-BUILT) + 7.
       DIVIDE FIRST-PART BY 2X2 GIVING WORKING-NUMBER 
         REMAINDER RANDOM-NUMBER-BUILT. 
       IF RANDOM-NUMBER-BUILT > LOW-RANGE AND
          RANDOM-NUMBER-BUILT < (HIGH-RANGE + 1)
         GO TO 600-RANDGEN-CLEANUP.
       GO TO 400-RANDGEN-FORMULA.
  * *********************************************     
  *    GOOD RANDOM NUMBER HAS BEEN BUILT        *               
  * *********************************************
   600-RANDGEN-CLEANUP.
       ADD 1 TO COUNT-OF-ACCESSES.
       COMPUTE RANDOM-NUMBER = 
            RANDOM-NUMBER-BUILT - LOW-RANGE. 
  * *******************************************************
  * THE NEXT 3 LINE OF CODE ARE FOR TESTING  ON CONSOLE   *  
  * *******************************************************
       DISPLAY RANDOM-NUMBER.
       IF COUNT-OF-ACCESSES < RANDOM-NUMBERS-NEEDED
        GO TO 100-RANDGEN-EDIT-HOUSEKEEPING.     
   900-EXIT-RANDGEN.
       IF RANDOM-MSG NOT = SPACE
        DISPLAY 'RANDOM-MSG: ' RANDOM-MSG.
        MOVE ZERO TO COUNT-OF-ACCESSES RANDOM-NUMBERS-NEEDED RANDOM-NUMBER. 
        MOVE SPACE TO YOU-PROVIDE-SEED RUN-AGAIN.
       DISPLAY 'RUN AGAIN Y OR N '
         NO ADVANCING.
       ACCEPT RUN-AGAIN.
       IF (RUN-AGAIN = 'Y' OR 'y')
         GO TO 100-RANDGEN-EDIT-HOUSEKEEPING.
       ACCEPT PAUSE-FOR-A-SECOND.
       GOBACK.

Answer 15

Let's say you want to go over shuffled lists over and over, without having the O(n) delay each time you start over to shuffle it again, in that case we can do this:

1. Create 2 lists A and B, with 0 to 1000, takes 2n space.

2. Shuffle list A using Fisher-Yates, takes n time.

3. When drawing a number, do 1-step Fisher-Yates shuffle on the other list.

4. When cursor is at list end, switch to the other list.

Preprocess

cursor = 0

selector = A
other    = B

shuffle(A)

Draw

temp = selector[cursor]

swap(other[cursor], other[random])

if cursor == N
then swap(selector, other); cursor = 0
else cursor = cursor + 1

return temp

Answer 16

You could use a good pseudo-random number generator with 10 bits and throw away 1001 to 1023 leaving 0 to 1000.

From here we get the design for a 10 bit PRNG..

• 10 bits, feedback polynomial x^10 + x^7 + 1 (period 1023)

• use a Galois LFSR to get fast code

Answer 17

Another posibility:

You can use an array of flags. And take the next one when it;s already chosen.

But, beware after 1000 calls, the function will never end so you must make a safeguard.

Answer 18

Most of the answers here fail to guarantee that they won't return the same number twice. Here's a correct solution:

int nrrand(void) {
  static int s = 1;
  static int start = -1;
  do {
    s = (s * 1103515245 + 12345) & 1023;
  } while (s >= 1001);
  if (start < 0) start = s;
  else if (s == start) abort();

  return s;
}

I'm not sure that the constraint is well specified. One assumes that after 1000 other outputs a value is allowed to repeat, but that naively allows 0 to follow immediately after 0 so long as they both appear at the end and start of sets of 1000. Conversely, while it's possible to keep a distance of 1000 other values between repetitions, doing so forces a situation where the sequence replays itself in exactly the same way every time because there's no other value that has occurred outside of that limit.

Here's a method that always guarantees at least 500 other values before a value can be repeated:

int nrrand(void) {
  static int h[1001];
  static int n = -1;

  if (n < 0) {
    int s = 1;
    for (int i = 0; i < 1001; i++) {
      do {
        s = (s * 1103515245 + 12345) & 1023;
      } while (s >= 1001);
      /* If we used `i` rather than `s` then our early results would be poorly distributed. */
      h[i] = s;
    }
    n = 0;
  }

  int i = rand(500);
  if (i != 0) {
      i = (n + i) % 1001;
      int t = h[i];
      h[i] = h[n];
      h[n] = t;
  }
  i = h[n];
  n = (n + 1) % 1001;

  return i;
}

Answer 19

When N is greater than 1000 and you need to draw K random samples you could use a set that contains the samples so far. For each draw you use rejection sampling, which will be an "almost" O(1) operation, so the total running time is nearly O(K) with O(N) storage.

This algorithm runs into collisions when K is "near" N. This means that running time will be a lot worse than O(K). A simple fix is to reverse the logic so that, for K > N/2, you keep a record of all the samples that have not been drawn yet. Each draw removes a sample from the rejection set.

The other obvious problem with rejection sampling is that it is O(N) storage, which is bad news if N is in the billions or more. However, there is an algorithm that solves that problem. This algorithm is called Vitter's algorithm after it's inventor. The algorithm is described here. The gist of Vitter's algorithm is that after each draw, you compute a random skip using a certain distribution which guarantees uniform sampling.

Answer 20

Fisher Yates

for i from n−1 downto 1 do
     j ← random integer such that 0 ≤ j ≤ i
     exchange a[j] and a[i]

It is actually O(n-1) as you only need one swap for the last two
This is C#

public static List<int> FisherYates(int n)
{
    List<int> list = new List<int>(Enumerable.Range(0, n));
    Random rand = new Random();
    int swap;
    int temp;
    for (int i = n - 1; i > 0; i--)
    {
        swap = rand.Next(i + 1);  //.net rand is not inclusive
        if(swap != i)  // it can stay in place - if you force a move it is not a uniform shuffle
        {
            temp = list[i];
            list[i] = list[swap];
            list[swap] = temp;
        }
    }
    return list;
}

Answer 21

Please see my answer at https://stackoverflow.com/a/46807110/8794687

It is one of the simplest algorithms that have average time complexity O(s log s), s denoting the sample size. There are also some links there to hash table algorithms who's complexity is claimed to be O(s).

Answer 22

Someone posted "creating random numbers in excel". I am using this ideal. Create a structure with 2 parts, str.index and str.ran; For 10 random numbers create an array of 10 structures. Set the str.index from 0 to 9 and str.ran to different random number.

for(i=0;i<10; ++i) {
      arr[i].index = i;
      arr[i].ran   = rand();
}

Sort the array on the values in arr[i].ran. The str.index is now in a random order. Below is c code:

#include <stdio.h>
#include <stdlib.h>

struct RanStr { int index; int ran;};
struct RanStr arr[10];

int sort_function(const void *a, const void *b);

int main(int argc, char *argv[])
{
   int cnt, i;

   //seed(125);

   for(i=0;i<10; ++i)
   {
      arr[i].ran   = rand();
      arr[i].index = i;
      printf("arr[%d] Initial Order=%2d, random=%d\n", i, arr[i].index, arr[i].ran);
   }

   qsort( (void *)arr, 10, sizeof(arr[0]), sort_function);
   printf("\n===================\n");
   for(i=0;i<10; ++i)
   {
      printf("arr[%d] Random  Order=%2d, random=%d\n", i, arr[i].index, arr[i].ran);
   }

   return 0;
}

int sort_function(const void *a, const void *b)
{
   struct RanStr *a1, *b1;

   a1=(struct RanStr *) a;
   b1=(struct RanStr *) b;

   return( a1->ran - b1->ran );
}